The Correct Answer and Explanation is:
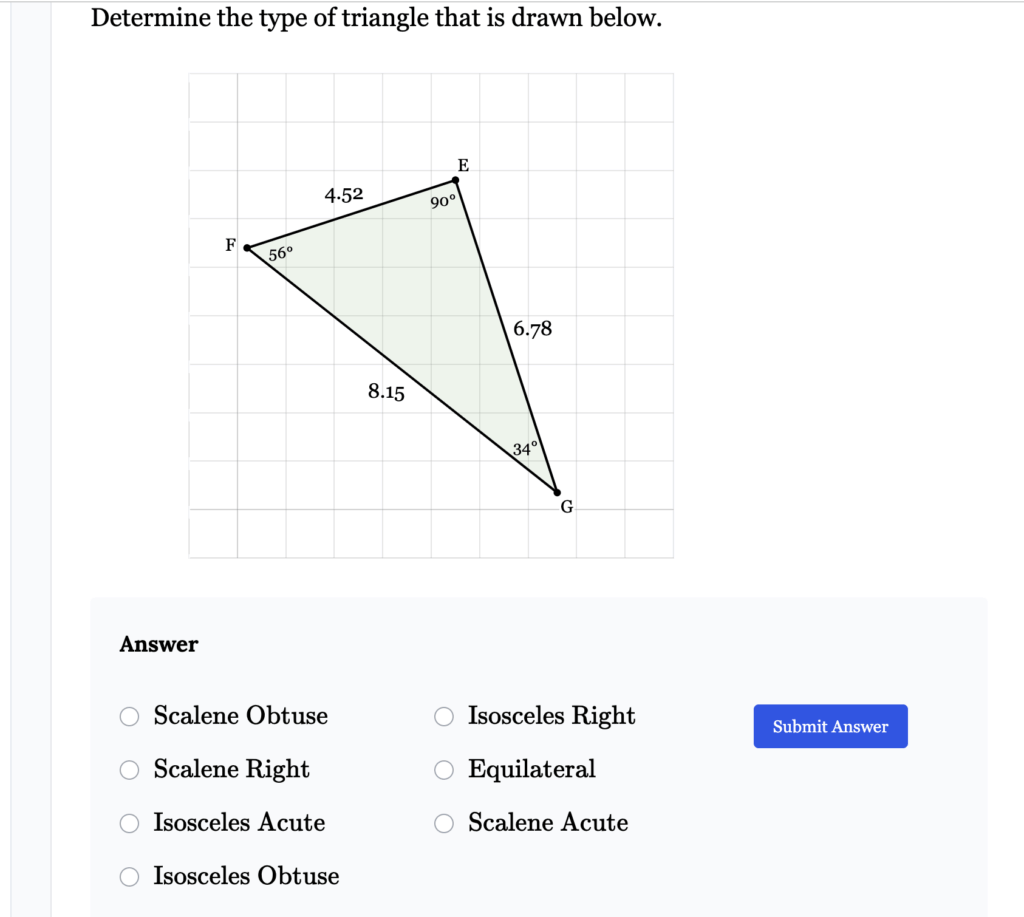
The triangle in the image is Scalene Right.
Explanation:
To classify the triangle, we analyze its sides and angles:
Step 1: Check the angles
The triangle has the following angles:
- ∠FEG = 90°
- ∠EFG = 56°
- ∠EGF = 34°
Since one angle is exactly 90°, this is a right triangle by definition.
Step 2: Check the sides
The side lengths are:
- FG = 8.15
- EF = 4.52
- EG = 6.78
All three sides have different lengths, meaning the triangle is scalene (a triangle with all sides of different lengths).
Step 3: Triangle type conclusion
- Since the triangle has one 90° angle → Right Triangle
- Since all three sides are of different lengths → Scalene Triangle
Therefore, the triangle is a Scalene Right Triangle.
Why other options are incorrect:
- Scalene Obtuse: This would require one angle to be greater than 90°, which it is not.
- Isosceles Right: Would require two sides of equal length and a 90° angle. The sides are not equal.
- Equilateral: All sides and all angles would need to be equal, which is not the case.
- Isosceles Acute/Obtuse: Would require two sides of equal length and no 90° angle (acute or one angle > 90°).
- Scalene Acute: All angles would need to be less than 90°, but one is exactly 90°.
Final Answer:
✅ Scalene Right
