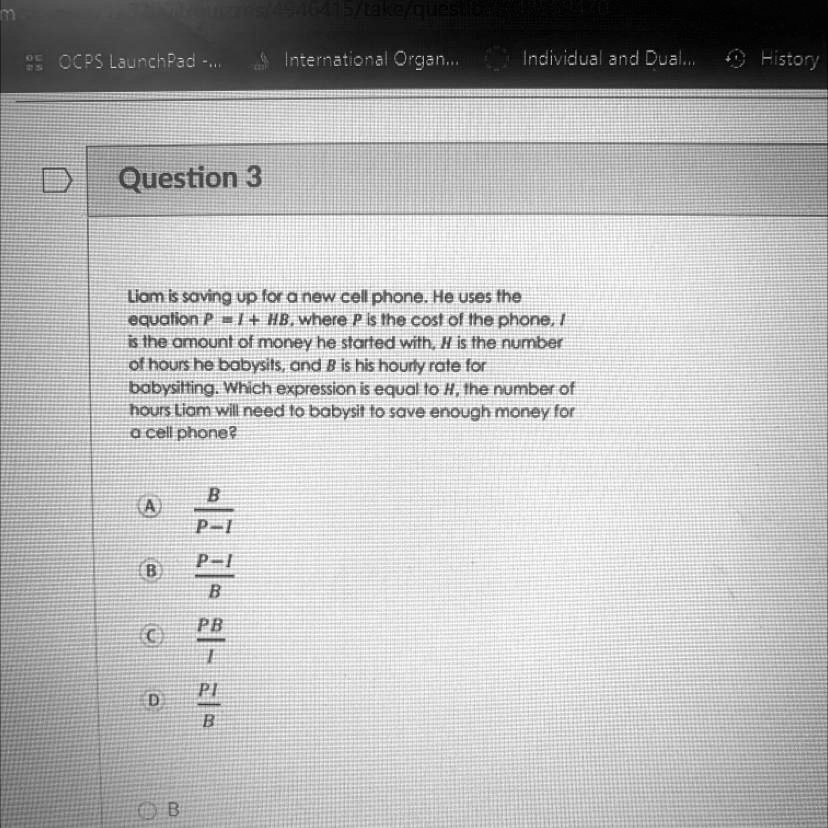
Liam is saving up for a new cell phone. He uses the equation
, where P is the cost of the phone, I is the amount of money he started with, H is the number of hours he babysits, and B is his hourly rate for babysitting. Which expression is equal to H, the number of hours Liam will need to babysit to save enough money for a cell phone?
The Correct Answer and Explanation is:
Correct expression (Choice B): P−IB\displaystyle \frac{P-I}{B}
Think of the equation P=I+HBP = I + HB as Liam’s budget line. P, in dollars, is the price of the phone. I is the dollars already in his piggy-bank. H is the unknown number of babysitting hours, and B is the dollar amount he earns each hour.
Solve for H by performing two inverse operations.
- Remove the initial money: subtract I from both sides. That leaves P−I=HBP − I = HB.
The difference P−IP − I is the additional money he still needs.
- Undo the multiplication by B: divide both sides by B. (P−I)/B=H(P − I)/B = H,
or written more naturally,
H=(P−I)/BH = (P − I)/B.
The fraction matches everyday reasoning. First calculate how many dollars remain to be earned (price minus current savings). Then see how many hours of work are required by dividing that dollar amount by dollars per hour. Because the numerator is measured in dollars and the denominator is measured in dollars per hour, the units cancel cleanly to give hours, confirming that the derived expression is dimensionally consistent.
A quick check validates the algebra. Substitute (P−I)/B(P − I)/B for H in the original equation:
I+B×[(P−I)/B]=I+(P−I)=PI + B \times [(P − I)/B] = I + (P − I) = P.
Since the equation balances, the rearrangement is correct.
Scan the multiple-choice options. Choice A, B/(P−I)B/(P − I), places B wrongly in the numerator. Choice C, PB/IPB/I, multiplies instead of subtracting I. Choice D, PI/BPI/B, multiplies P and I, which has no logical meaning here. Only choice B, (P−I)/B(P − I)/B, aligns with the derived expression.
Thus Liam must babysit
H=(P−I)/BH = (P − I)/B
hours to earn enough for the new phone. If Liam cannot work fractional hours, he should round this figure up to the next hour—or to the nearest hour.
