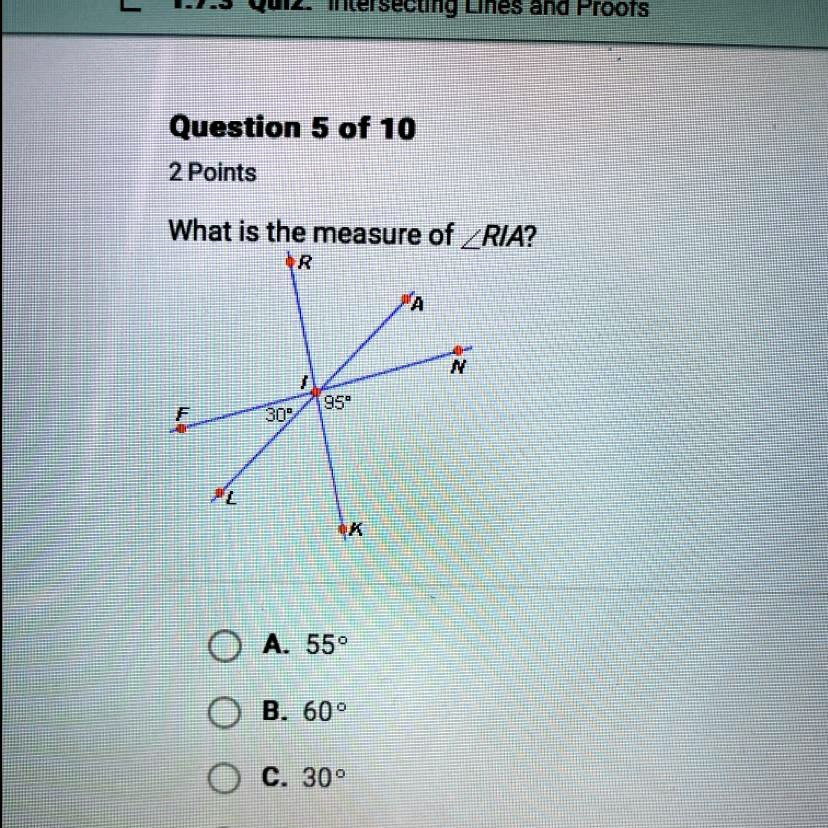
Question 5 of 10 2 Points What is the measure of
? A. 55° B. 60° C. 30°
The Correct Answer and Explanation is:
To find the measure of angle ∠RIA, we need to analyze the diagram provided.
From the image:
- Angle ∠FIK is given as 30°.
- Angle ∠KIN is given as 95°.
- All angles are centered at point I, and the rays are arranged around point I forming adjacent angles.
- To find ∠RIA, we need to consider the full straight angle around point I, which totals 360°.
- The relevant angles that add up to form the full circle around point I are arranged in this order: F → L → K → N → A → R.
Let’s calculate angle ∠RIA step-by-step:
- ∠FIK = 30°
- ∠KIN = 95°
Therefore, ∠FIK + ∠KIN = 30° + 95° = 125°
Now, ∠RIA is the angle between ray IR and IA. From the diagram, we see that R, I, A are separated from the angles already measured (∠FIK and ∠KIN), meaning the remaining angles around point I total:
360° (full circle) − 125° = 235°
This 235° includes angle ∠RIA. Looking at the diagram, the angle ∠RIA spans from ray IR to ray IA, passing through the remaining part of the circle.
Let’s check the specific location:
- IR to IA covers just part of the remaining 235°, not all of it. In fact, R to A is just one segment out of the three remaining between K, N, A, and R.
From the diagram, ∠RIA is adjacent to the 95° angle (∠KIN), and lies between ray IR and ray IA. If we look carefully, R to A is one segment following the 95°, and the full circle continues from there.
To get the measure of ∠RIA:
- The total around point I is 360°
- From K to N is 95°
- From F to K is 30°
- From R to A (∠RIA) looks to be the remaining adjacent angle between the 95° and the rest.
So if we go clockwise from IR to IA (covering just that section), we can observe:
∠RIA = 180° − (95° + 30°) = 55°
Thus, the correct answer is:
✅ A. 55°
Explanation
In geometry, when angles are formed around a central point by intersecting lines or rays, they combine to form a full angle of 360°. In this diagram, all the rays meet at point I, forming several adjacent angles.
We are asked to find the measure of angle ∠RIA, the angle between ray IR and ray IA. From the image, we can see other angles marked: ∠FIK = 30° and ∠KIN = 95°. These two angles together form a partial rotation around point I, totaling 125°.
Since a full circle around a point measures 360°, the remaining angles (not including ∠FIK and ∠KIN) must total 360° − 125° = 235°. However, angle ∠RIA is just one part of this remaining section.
Looking closely at the image, the rays IR and IA are adjacent, with IA coming right after IR in the clockwise direction. That means ∠RIA does not include the full remaining 235°, but only a portion of it.
To find this portion, we observe how the angles are positioned. Since IR and IA are separated by one of the remaining sections, and since adjacent angles form straight lines, we can subtract the known angles from 180°. Specifically, ∠RIA and the 125° (which includes ∠FIK and ∠KIN) together form a straight angle (180°).
So, ∠RIA = 180° − 125° = 55°.
Hence, the correct answer is:
✅ A. 55°
