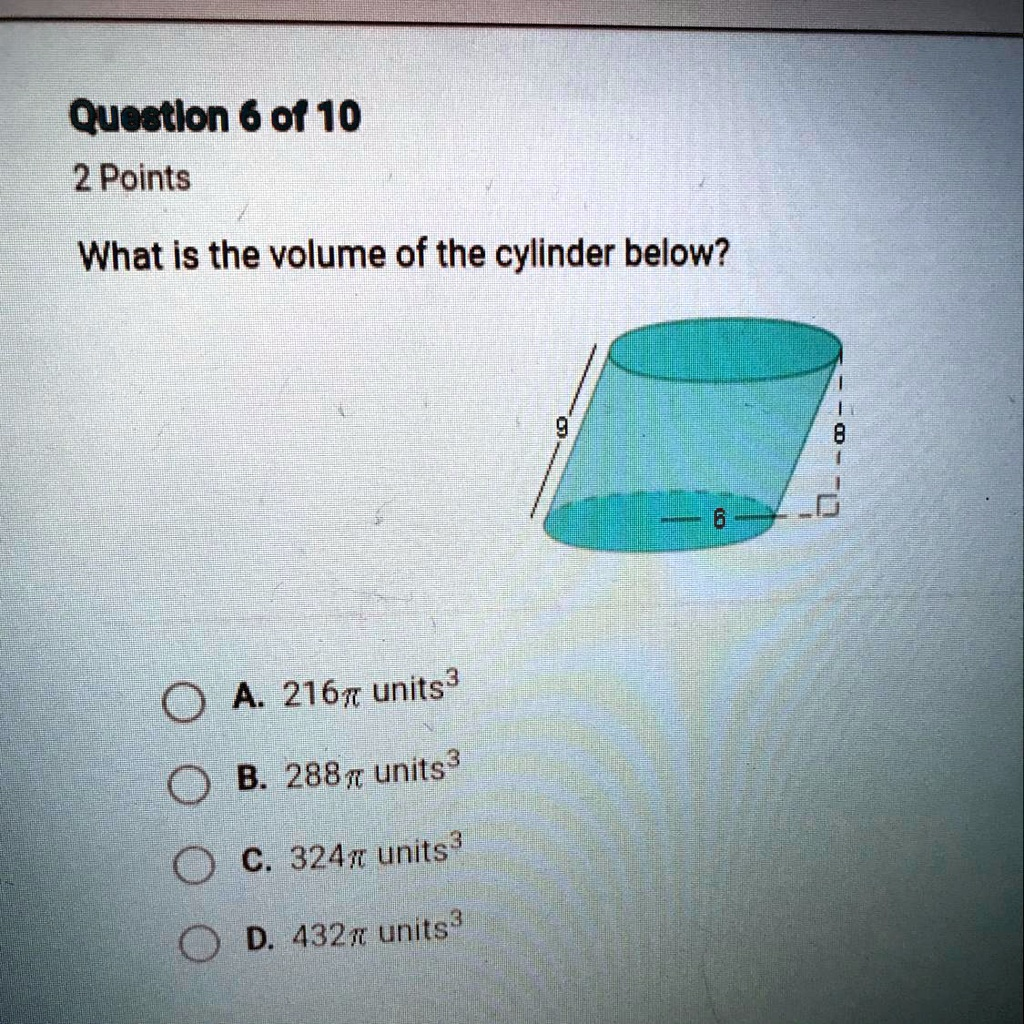
Question 6 of 10 2 Points What is the volume of the cylinder below? A.
units
B.
units
C.
units
D.
units
The Correct Answer and Explanation is:
To find the volume of a cylinder, we use the formula: V=πr2hV = \pi r^2 h
Where:
- rr is the radius of the base,
- hh is the height (perpendicular distance between the bases),
- π\pi is the constant Pi (approximately 3.1416).
From the image:
- Radius r=6r = 6 units
- Height h=8h = 8 units (not the slant height of 9, because volume uses the vertical height)
Step-by-step Calculation:
- Square the radius: r2=62=36r^2 = 6^2 = 36
- Multiply by the height: 36×8=28836 \times 8 = 288
- Multiply by π\pi: V=288π units3V = 288\pi \, \text{units}^3
Final Answer:
B. 288π units³
Explanation
To compute the volume of a cylinder, it’s important to use the correct geometric parameters. The volume of a cylinder is calculated by the product of the area of its circular base and its height. In this question, the base is a circle with a radius of 6 units. The area of a circle is given by πr2\pi r^2, so for this cylinder, the area of the base is π×62=36π\pi \times 6^2 = 36\pi square units.
Next, we must multiply this base area by the height of the cylinder. The image shows a slanted cylinder, but the height required for the volume formula is the vertical height—the perpendicular distance between the two circular bases—which is marked as 8 units in the diagram. The slant height of 9 units is not used in the volume calculation.
Therefore, the volume becomes 36π×8=288π36\pi \times 8 = 288\pi cubic units. This shows that the shape of the cylinder doesn’t affect the volume as long as the height is measured perpendicularly between the bases. Whether the cylinder is straight or slanted, the formula remains the same as long as the correct vertical height is used.
Thus, the correct answer is B. 288π units³, which accurately reflects the application of the volume formula using the given dimensions

.