x^2 + n SSxx SSxx 2. Show that (X’X)^-1 = in simple linear regression 3. 1 SSxx SSxx
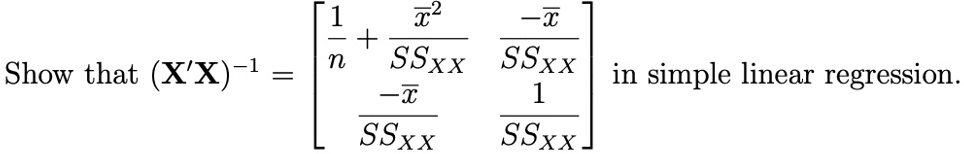
The Correct Answer and Explanation is:
To show that (X′X)−1=[1n+xˉ2SSXX−xˉSSXX−xˉSSXX1SSXX](\mathbf{X}’\mathbf{X})^{-1} = \begin{bmatrix} \frac{1}{n} + \frac{\bar{x}^2}{SS_{XX}} & -\frac{\bar{x}}{SS_{XX}} \\ -\frac{\bar{x}}{SS_{XX}} & \frac{1}{SS_{XX}} \end{bmatrix}
in simple linear regression, let’s walk through the derivation.
Step 1: Simple Linear Regression Design Matrix
In simple linear regression, we model: yi=β0+β1xi+εiy_i = \beta_0 + \beta_1 x_i + \varepsilon_i
The design matrix X\mathbf{X} is: X=[1x11x2⋮⋮1xn],size n×2\mathbf{X} = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \\ \end{bmatrix}, \quad \text{size } n \times 2
Then, X′X\mathbf{X}’\mathbf{X} is: X′X=[n∑xi∑xi∑xi2]=[nnxˉnxˉ∑xi2]\mathbf{X}’\mathbf{X} = \begin{bmatrix} n & \sum x_i \\ \sum x_i & \sum x_i^2 \\ \end{bmatrix} = \begin{bmatrix} n & n\bar{x} \\ n\bar{x} & \sum x_i^2 \\ \end{bmatrix}
Step 2: Define SSXXSS_{XX}
SSXX=∑(xi−xˉ)2=∑xi2−nxˉ2SS_{XX} = \sum (x_i – \bar{x})^2 = \sum x_i^2 – n\bar{x}^2
Step 3: Invert X′X\mathbf{X}’\mathbf{X}
We want to find: (X′X)−1=[nnxˉnxˉ∑xi2]−1(\mathbf{X}’\mathbf{X})^{-1} = \left[ \begin{array}{cc} n & n\bar{x} \\ n\bar{x} & \sum x_i^2 \\ \end{array} \right]^{-1}
Use the inverse of a 2×2 matrix:
If A=[abcd]A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, then A−1=1ad−bc[d−b−ca]A^{-1} = \frac{1}{ad – bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}
Apply this to X′X\mathbf{X}’\mathbf{X}:
- a=na = n
- b=nxˉb = n\bar{x}
- d=∑xi2d = \sum x_i^2
Then: det(X′X)=n∑xi2−n2xˉ2=n(∑xi2−nxˉ2)=nSSXX\det(\mathbf{X}’\mathbf{X}) = n \sum x_i^2 – n^2 \bar{x}^2 = n (\sum x_i^2 – n\bar{x}^2) = n SS_{XX}
Thus, (X′X)−1=1nSSXX[∑xi2−nxˉ−nxˉn](\mathbf{X}’\mathbf{X})^{-1} = \frac{1}{n SS_{XX}} \begin{bmatrix} \sum x_i^2 & -n\bar{x} \\ -n\bar{x} & n \end{bmatrix}
Now simplify each entry:
Top-left: ∑xi2nSSXX=nxˉ2+SSXXnSSXX=xˉ2SSXX+1n\frac{\sum x_i^2}{n SS_{XX}} = \frac{n\bar{x}^2 + SS_{XX}}{n SS_{XX}} = \frac{\bar{x}^2}{SS_{XX}} + \frac{1}{n}
Top-right and bottom-left: −nxˉnSSXX=−xˉSSXX\frac{-n\bar{x}}{n SS_{XX}} = -\frac{\bar{x}}{SS_{XX}}
Bottom-right: nnSSXX=1SSXX\frac{n}{n SS_{XX}} = \frac{1}{SS_{XX}}
Final Result:
(X′X)−1=[1n+xˉ2SSXX−xˉSSXX−xˉSSXX1SSXX](\mathbf{X}’\mathbf{X})^{-1} = \begin{bmatrix} \frac{1}{n} + \frac{\bar{x}^2}{SS_{XX}} & -\frac{\bar{x}}{SS_{XX}} \\ -\frac{\bar{x}}{SS_{XX}} & \frac{1}{SS_{XX}} \end{bmatrix}
Explanation (Summary)
This derivation uses the structure of the design matrix in simple linear regression and the formula for the inverse of a 2×2 matrix. We rewrite the sums using sample mean xˉ\bar{x} and the corrected sum of squares SSXXSS_{XX} to express the inverse in terms familiar in regression analysis. This matrix plays a key role in computing the variance-covariance matrix of the estimated coefficients and thus is fundamental in statistical inference.
