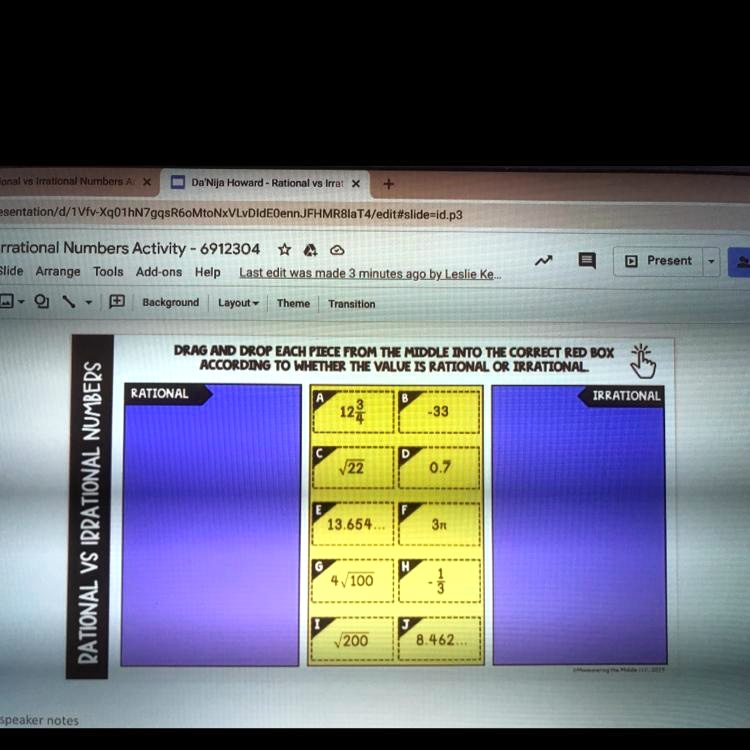
FROM THE MIDDLE INTO THE CORRECT RED BOX ACCORDING TO WHETHER THE VALUE IS RATIONAL OR IRRATIONAL RATIONAL A
B -33 C
D 0.7 E 13.654… F
G
H
I
J 8.462… IRRATIONAL
rrational Numbers Activity – 6912304 DRAG AND DROP EACH PIECE FROM THE MIDDLE INTO THE CORRECT RED BOX ACCORDING TO WHETHER THE VALUE IS RATIONAL OR IRRATIONAL RATIONAL A
B -33 C
D 0.7 E 13.654… F
G
H
I
J 8.462… IRRATIONAL
The Correct Answer and Explanation is:
✅ Correct Answers:
RATIONAL Numbers (can be expressed as a fraction or have a terminating/repeating decimal):
- A. 12¾ → Rational (Mixed number = 51/4)
- B. -33 → Rational (Integer = -33/1)
- D. 0.7 → Rational (Terminating decimal = 7/10)
- E. 13.654 → Rational (Terminating decimal = 13654/1000)
- G. 4√100 → Rational (√100 = 10 → 4 × 10 = 40)
- H. -⅓ → Rational (Fraction = -1/3)
- J. 8.462 → Rational (Terminating decimal = 8462/1000)
IRRATIONAL Numbers (non-repeating, non-terminating decimals or roots of non-perfect squares):
- C. √22 → Irrational (√22 ≈ 4.690… does not repeat or terminate)
- F. 3π → Irrational (π is irrational → 3π is irrational)
- I. √200 → Irrational (√200 ≈ 14.142… not a perfect square)
🧠 Explanation (300 Words):
The classification of numbers into rational and irrational is fundamental in mathematics.
A rational number is any number that can be written as a fraction of two integers, where the denominator is not zero. This includes:
- Whole numbers (e.g., -33),
- Fractions (like -⅓ or 12¾),
- Terminating decimals (e.g., 0.7 or 8.462),
- And repeating decimals.
In this activity:
- 12¾ is a mixed number which is equivalent to 51/4, so it is rational.
- -33, an integer, is rational.
- 0.7, 13.654, and 8.462 are all terminating decimals, which can be expressed as fractions.
- -⅓ is already a fraction.
- 4√100 simplifies to 4 × 10 = 40, which is also rational.
On the other hand, an irrational number cannot be written as a fraction. These numbers have non-terminating and non-repeating decimals. Common examples include:
- Square roots of non-perfect squares (like √22 or √200)
- Irrational constants like π
In this exercise:
- √22 and √200 are irrational because 22 and 200 are not perfect squares, so their square roots are infinite non-repeating decimals.
- 3π is irrational because π itself is irrational, and multiplying it by a rational number does not make it rational.
Recognizing whether a number is rational or irrational helps in algebra, calculus, and real-world measurements. It also reinforces understanding of number properties and how they behave within mathematical operations.
