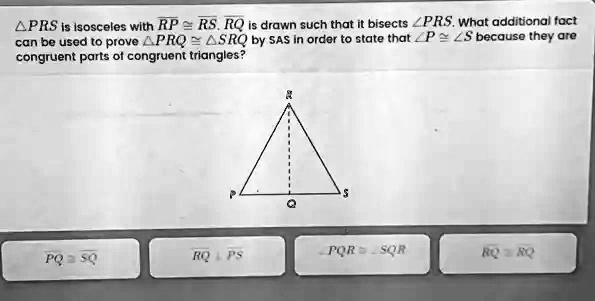
\triangle PRS is isosceles with \overline{RP} \cong \overline{RS}. \overline{RQ} is drawn such that it bisects \angle PRS. What additional fact can be used to prove \triangle PRQ \cong \triangle SRQ by SAS in order to state that \angle P \cong \angle S because they are congruent parts of congruent triangles?
The Correct Answer and Explanation is:
Correct Answer:
RQ ≅ RQ
Explanation
To determine the correct answer, let’s analyze the problem step by step.
We are given that triangle PRS is isosceles with RP ≅ RS. This means two sides of the triangle are congruent, indicating that angles opposite those sides will also be congruent if we can prove corresponding triangles are congruent.
Next, a segment RQ is drawn such that it bisects ∠PRS, which means ∠PRQ ≅ ∠SRO. This provides one pair of congruent angles between triangles PRQ and SRQ.
Now, we are tasked with identifying an additional fact needed to prove ΔPRQ ≅ ΔSRQ using the Side-Angle-Side (SAS) congruence postulate. The SAS postulate requires two sides and the included angle of one triangle to be congruent to two sides and the included angle of another triangle.
So far, we have:
- RP ≅ RS (Given)
- ∠PRQ ≅ ∠SRQ (Given, since RQ bisects ∠PRS)
For SAS, we need to establish that the side RQ ≅ RQ, which is the included side between those angles. This is a reflexive property, where a segment is always congruent to itself. This fact completes the required three components for SAS:
- RP ≅ RS (Given)
- ∠PRQ ≅ ∠SRQ (Angle bisector)
- RQ ≅ RQ (Reflexive property)
With these, we can now use SAS to prove ΔPRQ ≅ ΔSRQ.
Since the triangles are congruent, all their corresponding parts are congruent as well. Thus, ∠P ≅ ∠S, because they are corresponding angles of congruent triangles.
Therefore, the correct and necessary additional fact is:
RQ ≅ RQ.
