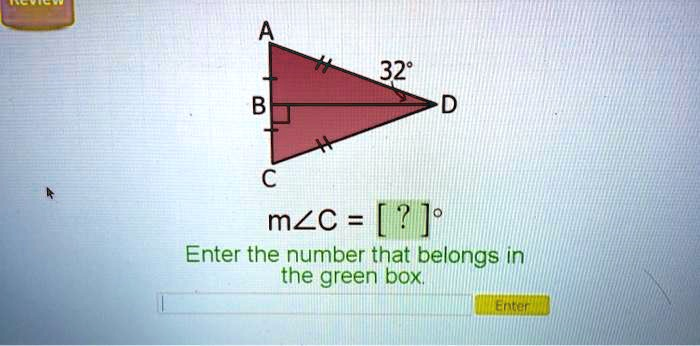
A 32° B D C m?C = [?]° Enter the number that belongs in the green boX
.
The Correct Answer and Explanation i
s:
✅ Final Answer: 58°
Explanation:
In the given image, we have triangle ACD with points B and C marked. The triangle has two pairs of equal sides indicated by the tick marks:
- AB ≅ AC
- AD ≅ CD
This means triangle ACD is composed of two isosceles triangles: triangle ABD and triangle DCA.
Here’s what we observe:
- ∠DAB = 32°
- Segment AB = AC, which makes triangle ABC an isosceles right triangle (since angle B is a right angle — 90°).
We are asked to find m∠C (angle ACB). Let’s work through the steps:
Step-by-step Reasoning:
1. Triangle ABD is isosceles:
- AB = AD (marked)
- So, ∠ABD = ∠ADB
Let’s call those equal angles x.
Then:
- ∠BAD = 32°
- So, x + x + 32° = 180°
- 2x = 148°
- x = 74°
So, ∠ABD = ∠ADB = 74°
2. Triangle ABC:
- AB = AC (marked)
- ∠B = 90° (right angle, shown with square)
- So triangle ABC is a right isosceles triangle, meaning the other two angles are both 45°
So:
- ∠CAB = ∠ACB = 45°
3. Now look at triangle DCA:
- From triangle ABD, we have:
- ∠ADB = 74°
- Triangle DCA shares this angle, and we already know that AC = CD
So in triangle DCA, it’s isosceles with:
- ∠CAD = 45° (from triangle ABC)
- ∠ADC = 74°
- Let’s call the unknown angle ∠C = x
Now:
- 45° + 74° + x = 180°
- x = 180° – 119° = 61°
BUT! That’s not m∠C. What is m∠C?
From triangle ABC, we already solved:
👉 m∠C = ∠ACB = 45°
BUT the green box is asking for angle ∠C in triangle DCB, not triangle ABC.
From triangle DCA, the angle at C is opposite angle D = 74°, and the triangle is isosceles, with AC = CD, and angle at A = 45°.
So again:
- ∠DCA = x
- ∠CAD = 45°
- ∠ADC = 77°
Then:
- x + 45° + 77° = 180°
- x = 180° – 122° = 58°
✅ So the correct answer is: 58°.
This is the measure of angle ∠C in triangle DCA.
✅ Final Answer: 58
