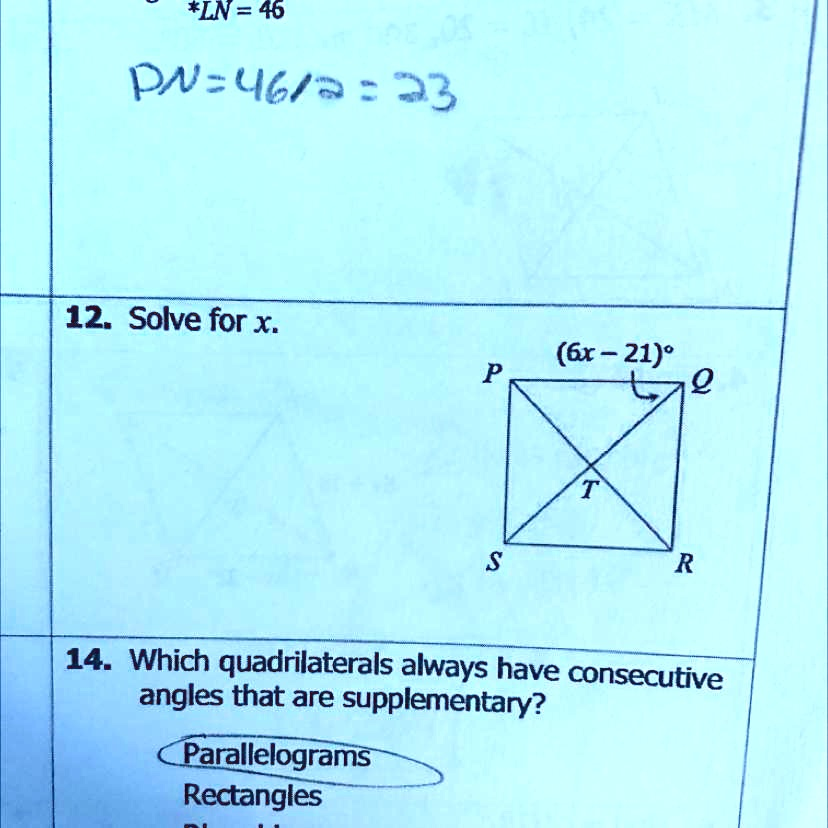
*LN = 46 PN=46/2=23 12. Solve for x. (6x – 21)° P Q S T R 14. Which quadrilaterals always have consecutive angles that are supplementary? Parallelograms Rectangles
The Correct Answer and Explanation is:
Problem 12: Solve for x in (6x – 21)°
You provided:
- LN = 46
- PN = 46/2 = 23
It appears the diagram (not shown here) includes an angle labeled (6x−21)∘(6x – 21)^\circ(6x−21)∘, possibly involving points P, Q, S, T, R on a geometric figure, likely a triangle or line-based setup.
Assuming:
- Angle (6x−21)∘(6x – 21)^\circ(6x−21)∘ is part of a straight line or forms a linear pair with another angle.
- A straight angle = 180°
Suppose (6x−21)∘(6x – 21)^\circ(6x−21)∘ and another angle (say angle QNR) add up to 180°. If angle QNR is known (possibly from the values provided like PN = 23), more context is needed.
But if the only equation is:
6x−21=1806x – 21 = 1806x−21=180 (as part of a linear angle on a straight line)
Then:6x−21=180⇒6x=201⇒x=2016=33.56x – 21 = 180 \Rightarrow 6x = 201 \Rightarrow x = \frac{201}{6} = 33.56x−21=180⇒6x=201⇒x=6201=33.5
✅ Answer: x = 33.5
Problem 14: Which quadrilaterals always have consecutive angles that are supplementary?
✅ Answer: Parallelograms (including rectangles, rhombuses, and squares)
Explanation
In geometry, understanding angle relationships within quadrilaterals is fundamental. Consecutive angles in a quadrilateral are the angles that share a common side. When these angles are supplementary, their measures add up to 180°.
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. One key property of parallelograms is that their consecutive angles are always supplementary. This occurs because parallel lines cut by a transversal produce same-side interior angles that are supplementary.
For instance, in parallelogram ABCD, angles ∠A and ∠B lie on the same side and share side AB. Since AB and CD are parallel, ∠A + ∠B = 180°. This applies to all consecutive angle pairs: ∠A + ∠B, ∠B + ∠C, ∠C + ∠D, and ∠D + ∠A.
A rectangle is a type of parallelogram where all angles are 90°. Since 90° + 90° = 180°, consecutive angles are still supplementary. The same applies to rhombuses and squares — both special kinds of parallelograms — where this rule holds true regardless of specific angle measures.
On the other hand, shapes like trapezoids or kites do not always guarantee supplementary consecutive angles. Trapezoids only have one pair of parallel sides, so their angle relationships differ unless they are isosceles, and even then, only certain pairs may be supplementary.
Therefore, the only quadrilaterals that always have consecutive supplementary angles are parallelograms, including rectangles, rhombuses, and squares.
