Challenge In Exercises 1, find each lettered angle measure.
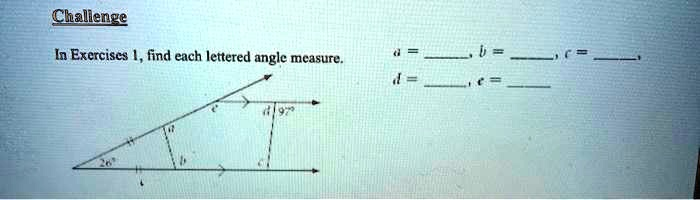
The Correct Answer and Explanation is:
Here are the final answers for each lettered angle measure:
a = 128°
b = 52°
c = 90°
d = 7°
e = 102°
Explanation
This geometry problem requires the application of several fundamental geometric principles, including the properties of isosceles triangles, parallel lines intersected by transversals, and supplementary angles. We will find the measure of each lettered angle in a logical sequence.
Step 1: Finding the measure of angle a
First, we focus on the triangle on the left side of the diagram. The tick marks on two of its sides indicate that they are equal in length, making it an isosceles triangle. A key property of an isosceles triangle is that the angles opposite the equal sides (the base angles) are also equal. One of these base angles is given as 26°. Therefore, the other base angle, which is adjacent to angle b, must also be 26°.
The sum of the interior angles in any triangle is 180°. Angle a is the third angle in this triangle. We can find its measure by subtracting the two known base angles from 180°.
- a = 180° – (26° + 26°)
- a = 180° – 52°
- a = 128°
Step 2: Finding the measure of angle b
Angle a and angle b lie on a straight line, which is the bottom parallel line. Angles that form a straight line are called a linear pair and are supplementary, meaning their sum is 180°.
- a + b = 180°
- 128° + b = 180°
- b = 180° – 128°
- b = 52°
Step 3: Finding the measure of angle e
The two horizontal lines are parallel. The slanted line that forms angle e acts as a transversal. Angle e and the interior angle at the bottom of the same transversal are consecutive interior angles. The total interior angle at the bottom is the sum of angle b and the adjacent 26° base angle.
- Interior angle = b + 26° = 52° + 26° = 78°
- Consecutive interior angles are supplementary.
- e + 78° = 180°
- e = 180° – 78°
- e = 102°
Step 4: Finding the measure of angle c
The small square symbol where the vertical line segment meets the bottom parallel line indicates a right angle. This means the line segment is perpendicular to the bottom line. Since the two horizontal lines are parallel, the vertical segment must also be perpendicular to the top line. Therefore, angle c is a right angle.
- c = 90°
Step 5: Finding the measure of angle d
The vertical line that forms angle d is perpendicular to the top parallel line, forming a 90° angle. The given 97° angle is composed of this 90° angle and angle d. To find d, we subtract the 90° angle from the total 97° angle.
- d + 90° = 97°
- d = 97° – 90°
- d = 7°
