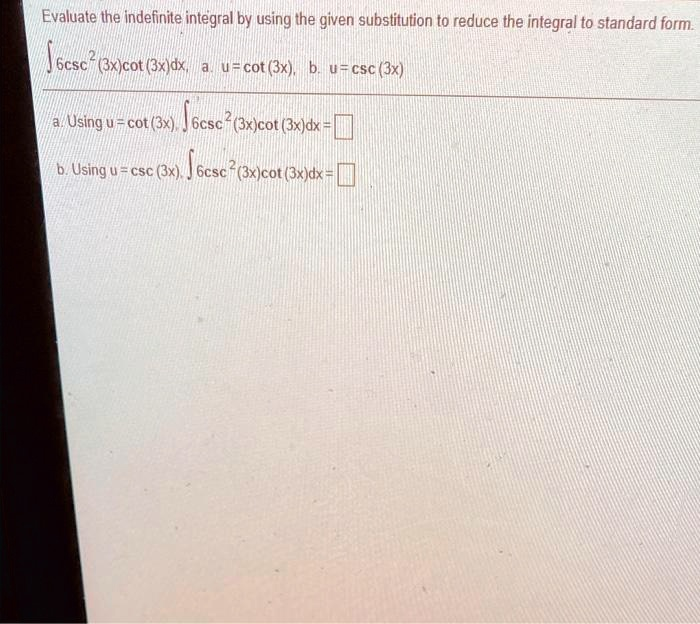
Evaluate the indefinite integral by using the given substitution to reduce the integral to standard form.\
, a.
, b.
\ a. Using
,
\ b. Using
,
The Correct Answer and Explanation is:
We are given the integral:∫6csc2(3x)cot(3x) dx\int 6 \csc^2(3x) \cot(3x)\, dx∫6csc2(3x)cot(3x)dx
We are to evaluate it using two different substitutions:
a. Using u=cot(3x)u = \cot(3x)u=cot(3x):
Step 1: Differentiate u=cot(3x)u = \cot(3x)u=cot(3x)dudx=−3csc2(3x)⇒du=−3csc2(3x) dx\frac{du}{dx} = -3 \csc^2(3x) \quad \Rightarrow \quad du = -3 \csc^2(3x) \, dxdxdu=−3csc2(3x)⇒du=−3csc2(3x)dx
Solve for csc2(3x) dx\csc^2(3x)\, dxcsc2(3x)dx:csc2(3x) dx=−13 du\csc^2(3x)\, dx = -\frac{1}{3} \, ducsc2(3x)dx=−31du
Now substitute into the integral:∫6csc2(3x)cot(3x) dx=∫6cot(3x)⋅csc2(3x) dx\int 6 \csc^2(3x) \cot(3x) \, dx = \int 6 \cot(3x) \cdot \csc^2(3x) \, dx∫6csc2(3x)cot(3x)dx=∫6cot(3x)⋅csc2(3x)dx
Substitute cot(3x)=u\cot(3x) = ucot(3x)=u, and csc2(3x) dx=−13du\csc^2(3x)\, dx = -\frac{1}{3} ducsc2(3x)dx=−31du:=∫6u⋅(−13) du=−2∫u du=−2⋅u22+C=−u2+C= \int 6u \cdot \left(-\frac{1}{3}\right) \, du = -2 \int u \, du = -2 \cdot \frac{u^2}{2} + C = -u^2 + C=∫6u⋅(−31)du=−2∫udu=−2⋅2u2+C=−u2+C
Substitute back u=cot(3x)u = \cot(3x)u=cot(3x):−cot2(3x)+C\boxed{-\cot^2(3x) + C}−cot2(3x)+C
b. Using u=csc(3x)u = \csc(3x)u=csc(3x):
Step 1: Differentiate u=csc(3x)u = \csc(3x)u=csc(3x)dudx=−3csc(3x)cot(3x)⇒du=−3csc(3x)cot(3x) dx\frac{du}{dx} = -3 \csc(3x) \cot(3x) \quad \Rightarrow \quad du = -3 \csc(3x) \cot(3x) \, dxdxdu=−3csc(3x)cot(3x)⇒du=−3csc(3x)cot(3x)dx
Solve for csc(3x)cot(3x)dx\csc(3x) \cot(3x) dxcsc(3x)cot(3x)dx:csc(3x)cot(3x) dx=−13 du\csc(3x) \cot(3x)\, dx = -\frac{1}{3} \, ducsc(3x)cot(3x)dx=−31du
Now write the integral in terms of uuu:∫6csc2(3x)cot(3x) dx=∫6csc(3x)⋅csc(3x)cot(3x) dx\int 6 \csc^2(3x) \cot(3x) \, dx = \int 6 \csc(3x) \cdot \csc(3x) \cot(3x) \, dx∫6csc2(3x)cot(3x)dx=∫6csc(3x)⋅csc(3x)cot(3x)dx
Group: csc(3x)cot(3x) dx=−13du\csc(3x) \cot(3x)\, dx = -\frac{1}{3} ducsc(3x)cot(3x)dx=−31du, so:=∫6csc(3x)⋅(−13) du=−2∫u du=−u2+C= \int 6 \csc(3x) \cdot (-\frac{1}{3}) \, du = -2 \int u \, du = -u^2 + C=∫6csc(3x)⋅(−31)du=−2∫udu=−u2+C
Substitute back u=csc(3x)u = \csc(3x)u=csc(3x):−csc2(3x)+C\boxed{-\csc^2(3x) + C}−csc2(3x)+C
📘 Explanation
To evaluate the integral ∫6csc2(3x)cot(3x) dx\int 6 \csc^2(3x) \cot(3x)\, dx∫6csc2(3x)cot(3x)dx, we use u-substitution, a technique that simplifies a complex expression into a standard integral form.
In part (a), we let u=cot(3x)u = \cot(3x)u=cot(3x), a function whose derivative involves csc2(3x)\csc^2(3x)csc2(3x), which is present in the integrand. By differentiating uuu, we find du=−3csc2(3x)dxdu = -3 \csc^2(3x) dxdu=−3csc2(3x)dx. This tells us how to express part of the integrand in terms of dududu. When we rearrange, we get csc2(3x)dx=−13du\csc^2(3x) dx = -\frac{1}{3} ducsc2(3x)dx=−31du, and substitute into the integral. The original expression becomes ∫6u(−13)du=−2∫u du\int 6u(-\frac{1}{3}) du = -2 \int u\, du∫6u(−31)du=−2∫udu, a basic polynomial integral. Solving yields −u2+C-u^2 + C−u2+C, and substituting back gives −cot2(3x)+C-\cot^2(3x) + C−cot2(3x)+C.
In part (b), we instead use u=csc(3x)u = \csc(3x)u=csc(3x), another trigonometric identity involved in the integrand. Differentiating gives du=−3csc(3x)cot(3x)dxdu = -3 \csc(3x) \cot(3x) dxdu=−3csc(3x)cot(3x)dx, and solving gives csc(3x)cot(3x)dx=−13du\csc(3x)\cot(3x) dx = -\frac{1}{3} ducsc(3x)cot(3x)dx=−31du. The original integral is rewritten as ∫6csc(3x)⋅csc(3x)cot(3x)dx=∫6csc(3x)⋅(−13)du\int 6 \csc(3x) \cdot \csc(3x) \cot(3x) dx = \int 6 \csc(3x) \cdot (-\frac{1}{3}) du∫6csc(3x)⋅csc(3x)cot(3x)dx=∫6csc(3x)⋅(−31)du. This again reduces to a simple polynomial form: −2∫u du=−u2+C-2 \int u\, du = -u^2 + C−2∫udu=−u2+C. Replacing uuu yields the final result: −csc2(3x)+C-\csc^2(3x) + C−csc2(3x)+C.
Each method is valid and demonstrates the power of substitution for integrating complex trigonometric expressions.
