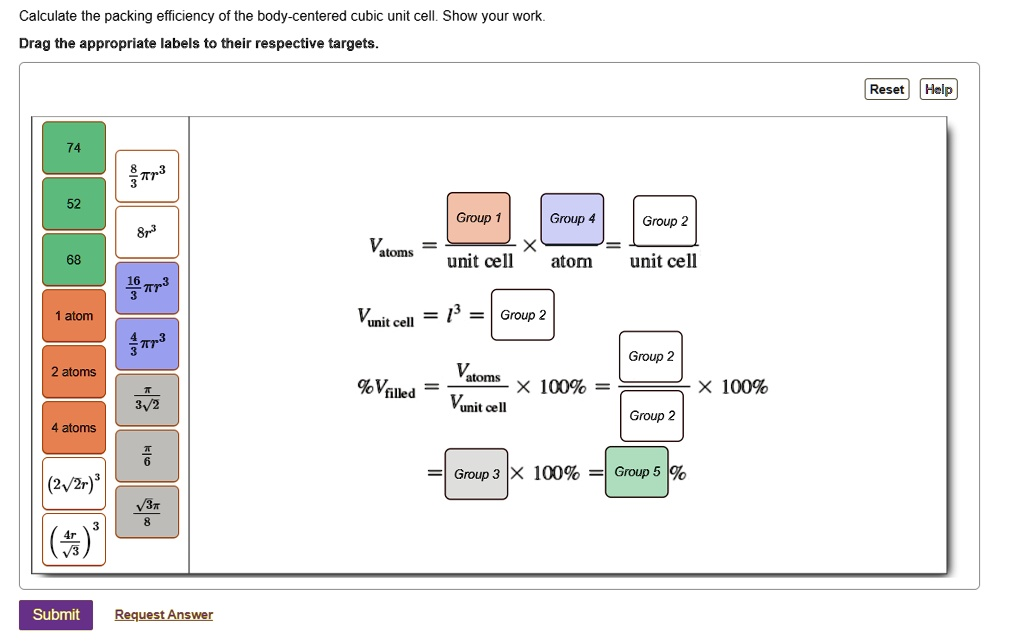
Calculate the packing efficiency of the body-centered cubic unit cell. Show your work. Drag the appropriate labels to their respective targets. 74
52
68
1 atom
2 atoms
4 atoms
Submit Request Answer Group 1 Group 4 Group 2
Group 2 Group 2 Group 2 %
Group 2
Reset Help
The Correct Answer and Explanation is:
Step-by-Step Explanation (Like a Textbook)
🔹 1. Understand the Structure
A BCC unit cell has:
- 2 atoms per unit cell (1 from the center, 1 from the corners combined)
- Atoms touch along the body diagonal of the cube.
🔹 2. Volume of Atoms in the Unit Cell (V_atoms)
Each atom has volume: Vatom=43πr3V_{\text{atom}} = \frac{4}{3}\pi r^3Vatom=34πr3
Since BCC has 2 atoms per unit cell: Vatoms=2×43πr3=83πr3V_{\text{atoms}} = 2 \times \frac{4}{3}\pi r^3 = \frac{8}{3}\pi r^3Vatoms=2×34πr3=38πr3
- ✅ Group 1: 2 atoms
- ✅ Group 4: 43πr3\frac{4}{3}\pi r^334πr3
- ✅ Group 2: 83πr3\frac{8}{3}\pi r^338πr3
🔹 3. Volume of the Unit Cell (V_unit cell)
Atoms in BCC touch along the body diagonal: body diagonal=4r=3l⇒l=4r3\text{body diagonal} = 4r = \sqrt{3}l \Rightarrow l = \frac{4r}{\sqrt{3}}body diagonal=4r=3l⇒l=34r
So, Vunit cell=l3=(4r3)3V_{\text{unit cell}} = l^3 = \left( \frac{4r}{\sqrt{3}} \right)^3Vunit cell=l3=(34r)3
- ✅ Group 2: (4r3)3\left(\frac{4r}{\sqrt{3}}\right)^3(34r)3
🔹 4. Packing Efficiency (%V_filled)
%Vfilled=VatomsVunit cell×100%=83πr3(4r3)3×100%\%\text{V}_{\text{filled}} = \frac{V_{\text{atoms}}}{V_{\text{unit cell}}} \times 100\% = \frac{\frac{8}{3}\pi r^3}{\left( \frac{4r}{\sqrt{3}} \right)^3} \times 100\%%Vfilled=Vunit cellVatoms×100%=(34r)338πr3×100%
Simplifying: =83πr364r333×100%=8π64/3×100%=π38×100%≈68%= \frac{\frac{8}{3}\pi r^3}{\frac{64r^3}{3\sqrt{3}}} \times 100\% = \frac{8\pi}{64/\sqrt{3}} \times 100\% = \frac{\pi \sqrt{3}}{8} \times 100\% \approx 68\%=3364r338πr3×100%=64/38π×100%=8π3×100%≈68%
- ✅ Group 3: π38\frac{\pi \sqrt{3}}{8}8π3
- ✅ Group 5: 68
✅ Final Label Placement
| Label | Goes To |
|---|---|
| Group 1 | 2 atoms |
| Group 4 | 43πr3\frac{4}{3} \pi r^334πr3 |
| Group 2 | 83πr3\frac{8}{3} \pi r^338πr3, (4r3)3\left(\frac{4r}{\sqrt{3}}\right)^3(34r)3 |
| Group 3 | π38\frac{\pi \sqrt{3}}{8}8π3 |
| Group 5 | 68 |
🧠 Concept Summary
- BCC has 2 atoms per unit cell.
- Packing efficiency is the fraction of unit cell volume occupied by atoms.
- The derivation involves using geometry (atoms touch along the diagonal) and volume formulas.
- Final packing efficiency of BCC is approximately 68%, meaning 68% of the space is filled with atoms while the rest is empty space.
