The integrated rate law for a third order reaction is \frac{1}{[A]_t^2} = \frac{1}{[A]_0^2} + 2kt Write an expression for the half life of a reactant in a third order reaction.
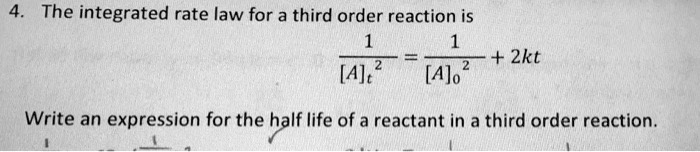
To find the half-life expression for a third-order reaction, we start from the integrated rate law:1[A]t2=1[A]02+2kt\frac{1}{[A]_t^2} = \frac{1}{[A]_0^2} + 2kt[A]t21=[A]021+2kt
At half-life t1/2t_{1/2}t1/2, the concentration [A]t=[A]02[A]_t = \frac{[A]_0}{2} [A]t=2[A]0. Plug this into the equation:1([A]02)2=1[A]02+2kt1/2\frac{1}{\left( \frac{[A]_0}{2} \right)^2} = \frac{1}{[A]_0^2} + 2k t_{1/2}(2[A]0)21=[A]021+2kt1/2
Simplify the left-hand side:1([A]024)=4[A]02\frac{1}{\left( \frac{[A]_0^2}{4} \right)} = \frac{4}{[A]_0^2}(4[A]02)1=[A]024
Now the equation becomes:4[A]02=1[A]02+2kt1/2\frac{4}{[A]_0^2} = \frac{1}{[A]_0^2} + 2k t_{1/2}[A]024=[A]021+2kt1/2
Subtract 1[A]02\frac{1}{[A]_0^2}[A]021 from both sides:3[A]02=2kt1/2\frac{3}{[A]_0^2} = 2k t_{1/2}[A]023=2kt1/2
Now solve for t1/2t_{1/2}t1/2:t1/2=32k[A]02t_{1/2} = \frac{3}{2k [A]_0^2}t1/2=2k[A]023
✅ Final Answer:
t1/2=32k[A]02\boxed{t_{1/2} = \frac{3}{2k [A]_0^2}}t1/2=2k[A]023
This is the half-life expression for a third-order reaction.
