Find the exact value of

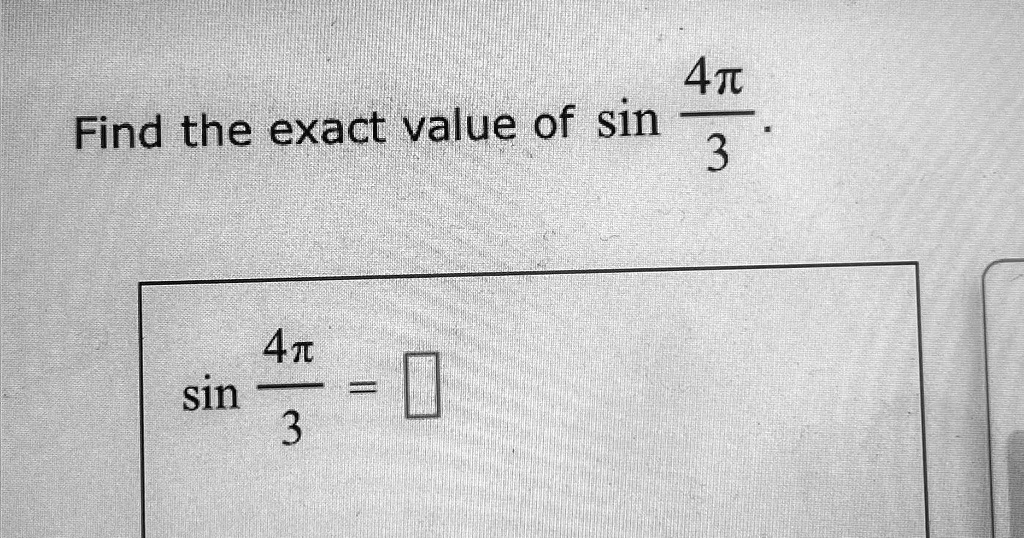
The Correct Answer and Explanation is:

To solve for the exact value of sin⁡(4π3)\sin\left(\frac{4\pi}{3}\right)sin(34π), we will follow a step-by-step trigonometric approach and explain each part clearly.

Step 1: Understand the Angle

The angle given is 4π3\frac{4\pi}{3}34π. This is a radian measure. To understand where it lies on the unit circle, we convert it to degrees:4π3×180∘π=240∘\frac{4\pi}{3} \times \frac{180^\circ}{\pi} = 240^\circ34π×π180∘=240∘

So, 4π3\frac{4\pi}{3}34π radians is equivalent to 240∘240^\circ240∘, which lies in the third quadrant.

Step 2: Reference Angle

In the third quadrant, the reference angle is found by subtracting 180∘180^\circ180∘ from the angle:240∘−180∘=60∘240^\circ – 180^\circ = 60^\circ240∘−180∘=60∘

This means that the reference angle is 60∘60^\circ60∘ (or π3\frac{\pi}{3}3π radians).

Step 3: Sign of the Sine Function

In the third quadrant, the sine function is negative because in the unit circle, y-values (which represent sine) are negative below the x-axis.

Step 4: Exact Value of sin⁡(60∘)\sin(60^\circ)sin(60∘)

From trigonometric values of special angles:sin⁡(60∘)=sin⁡(π3)=32\sin\left(60^\circ\right) = \sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}sin(60∘)=sin(3π)=23

Since our angle is in the third quadrant where sine is negative:sin⁡(4π3)=−32\sin\left(\frac{4\pi}{3}\right) = -\frac{\sqrt{3}}{2}sin(34π)=−23

Final Answer:

sin⁡(4π3)=−32\boxed{\sin\left(\frac{4\pi}{3}\right) = -\frac{\sqrt{3}}{2}}sin(34π)=−23

Conclusion:

To find the exact value of a trigonometric function for an angle in radians, we identify the quadrant in which the angle lies, determine the reference angle, use the known trigonometric values of that reference angle, and apply the correct sign based on the quadrant. In this case, since 4π3\frac{4\pi}{3}34π is in the third quadrant and the sine of π3\frac{\pi}{3}3π is 32\frac{\sqrt{3}}{2}23, we assign a negative sign to get the final answer −32-\frac{\sqrt{3}}{2}−23.