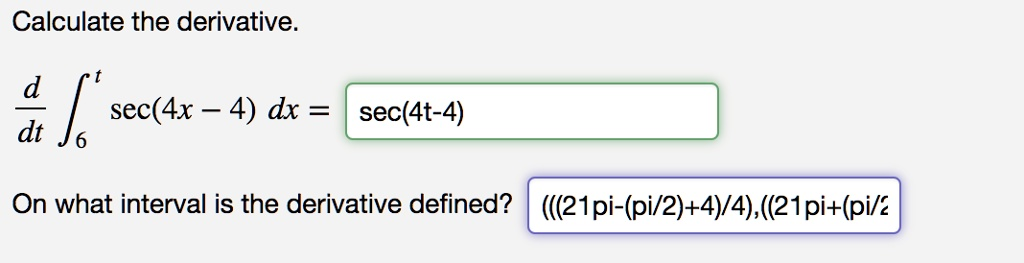
interval is the derivative defined?
Calculate the derivative.\
\ On what interval is the derivative defined?
The Correct Answer and Explanation is:
Here is the solution to the calculus problem
.
Derivative:
d/dt ∫[from 6 to t] sec(4x – 4) dx = sec(4t – 4)
Interval of Definition:
(1 + 11π/8, 1 + 13π/8)
Explanation
This problem requires a two-step solution. First, we calculate the derivative using the Fundamental Theorem of Calculus. Second, we determine the interval on which this derivative is defined by analyzing the continuity of the function involved.
Part 1: Calculating the Derivative
The problem asks for the derivative of an integral with a variable upper limit:
d/dt ∫[from 6 to t] sec(4x – 4) dx
To solve this, we use the Fundamental Theorem of Calculus, Part 1. The theorem states that if a function f is continuous on an interval containing a, then for any t in that interval, the function F(t) = ∫[from a to t] f(x) dx has a derivative F'(t) = f(t).
In this case:
- The function f(x) is the integrand, sec(4x – 4).
- The lower limit a is a constant, 6.
- The upper limit is the variable t.
Applying the theorem, we replace the variable x in the integrand with the upper limit t:
d/dt ∫[from 6 to t] sec(4x – 4) dx = sec(4t – 4)
Part 2: Finding the Interval of Definition
The result from the Fundamental Theorem of Calculus is valid only where the original integral is well-defined. The integral ∫[from a to b] f(x) dx is defined if the integrand f(x) is continuous on the interval of integration [a, b].
Our integrand is f(x) = sec(4x – 4). The secant function, sec(u), is undefined wherever cos(u) = 0. This occurs when u is an odd multiple of π/2. Therefore, sec(4x – 4) is discontinuous when:
4x – 4 = (2n + 1)π/2, where n is any integer.
Solving for x gives us the locations of the vertical asymptotes:
4x = 4 + (2n + 1)π/2
x = 1 + (2n + 1)π/8
The integral is defined only if the interval of integration, from 6 to t, does not contain any of these points of discontinuity. This means that t must be in the same continuous interval as the constant limit of integration, a = 6.
We need to find the interval of continuity (x_1, x_2) that contains x = 6. We can find the bracketing discontinuities by setting x = 6 in the equation for the asymptotes:
6 = 1 + (2n + 1)π/8
5 = (2n + 1)π/8
40/π = 2n + 1
Since 40/π ≈ 12.73, the odd integer (2n + 1) must be between 11 and 13.
- The lower bound of the interval corresponds to 2n + 1 = 11, which gives x = 1 + 11π/8.
- The upper bound of the interval corresponds to 2n + 1 = 13, which gives x = 1 + 13π/8.
The interval of continuity that contains x=6 is therefore (1 + 11π/8, 1 + 13π/8). The variable t must also lie in this interval. Thus, the derivative sec(4t – 4) is defined on the interval (1 + 11π/8, 1 + 13π/8).
