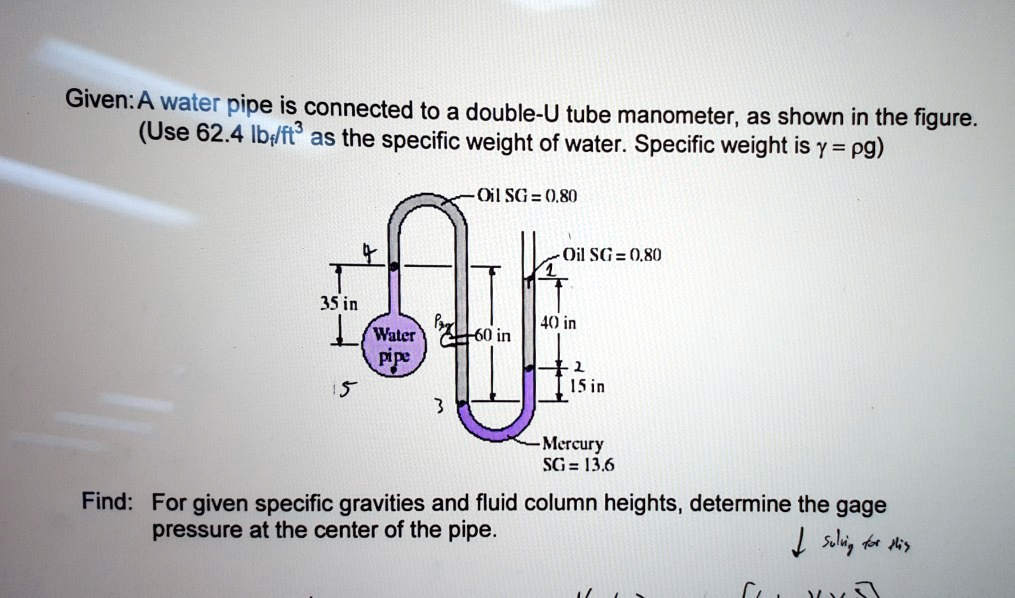
(Use 62.4 lb/ft3 as the specific weight of water. Specific weight is = pg) Oil SG=0.80 Oil SG=0.80 35 in /Water pipe S 40 in 60 in 15 in Mercury SG=13.6 Find: For given specific gravities and fluid column heights, determine the gauge pressure at the center of the pipe sling.
The Correct Answer and Explanation is:
Determination of Gage Pressure in a Water Pipe
Objective:
To determine the gage pressure at the center of the water pipe using the provided double-U tube manometer configuration.
Governing Principles:
The solution is based on the principles of hydrostatics. The pressure within a continuous, static fluid increases with depth. The change in pressure (ΔP) between two points is calculated using the formula ΔP = γh, where γ is the specific weight of the fluid and h is the vertical distance between the points.
To solve for an unknown pressure in a manometer system, one starts at a point of known pressure and moves through the fluid system to the point of unknown pressure, adding or subtracting the pressure change for each fluid column. Pressure increases when moving downward and decreases when moving upward. For gage pressure, the atmospheric pressure is considered the zero-reference point (P_atm = 0).
Analysis and Calculation:
- Identify Specific Weights:
The specific weights (γ) of the fluids are required. The specific weight of water is given.- Water: γ_water = 62.4 lbf/ft³
- Oil: γ_oil = SG_oil × γ_water = 0.80 × 62.4 lbf/ft³ = 49.92 lbf/ft³
- Mercury: γ_mercury = SG_mercury × γ_water = 13.6 × 62.4 lbf/ft³ = 848.64 lbf/ft³
- Formulate the Manometer Equation:
The calculation begins at the center of the water pipe (P_pipe) and proceeds through the manometer to the open end at point 1, which is at atmospheric pressure (P₁ = 0 gage). All height measurements must be converted from inches to feet by dividing by 12.The pressure equation is constructed by summing the pressure changes along the path:
P_pipe – (Pressure change from pipe to point 4) + (Pressure change from 4 to 3) – (Pressure change from 3 to 2) – (Pressure change from 2 to 1) = P₁- Pipe to Point 4: Moving up 35 in through oil. Pressure decreases.
ΔP = -γ_oil × (35/12 ft) - Point 4 to Point 3: Moving down 60 in through mercury. Pressure increases.
ΔP = +γ_mercury × (60/12 ft) - Point 3 to Point 2: Moving up 15 in through mercury. Pressure decreases.
ΔP = -γ_mercury × (15/12 ft) - Point 2 to Point 1: Moving up 40 in through oil. Pressure decreases.
ΔP = -γ_oil × (40/12 ft)
P_pipe – γ_oil(35/12) + γ_mercury(60/12) – γ_mercury(15/12) – γ_oil(40/12) = 0 - Pipe to Point 4: Moving up 35 in through oil. Pressure decreases.
- Solve for Pipe Pressure (P_pipe):
Rearrange the equation to solve for P_pipe and substitute the specific weight values.P_pipe = γ_oil(35/12) – γ_mercury(60/12) + γ_mercury(15/12) + γ_oil(40/12)
P_pipe = γ_oil(35/12 + 40/12) + γ_mercury(15/12 – 60/12)
P_pipe = γ_oil(75/12) – γ_mercury(45/12)Now, substitute the numerical values for specific weights and heights (in feet):
P_pipe = (49.92 lbf/ft³) × (6.25 ft) – (848.64 lbf/ft³) × (3.75 ft)
P_pipe = 312.0 lbf/ft² – 3182.4 lbf/ft²
P_pipe = -2870.4 lbf/ft² - Convert to Pounds per Square Inch (psi):
For a more conventional unit, convert the pressure from pounds per square foot (psf or lbf/ft²) to pounds per square inch (psi).
1 ft² = 144 in²P_pipe (psi) = P_pipe (lbf/ft²) / 144 in²/ft²
P_pipe (psi) = -2870.4 / 144
P_pipe ≈ -19.93 psi
Conclusion:
The gage pressure at the center of the water pipe is -2870.4 lbf/ft², which is equivalent to -19.93 psi. The negative sign indicates that the pressureometry. This involves starting at point P and moving through the connected tubes, adding or subtracting the pressure change due to each fluid column until we reach a point of known pressure. In this case, the known pressure is at the open end of the manometer (point 1), which is at atmospheric pressure. For gage pressure, we can set the atmospheric pressure to zero.
The fundamental equation for pressure change with depth is ΔP = γh, where γ is the specific weight of the fluid and h is the vertical height of the fluid column. Pressure increases as we move downward and decreases as we move upward.
Step-by-Step Solution
- Formulate the Manometer Equation:
We will write an equation for the pressure along the path from the center of the water pipe (P) to the open end of the manometer (point 1).P_pipe – γ_water(h_4-P) + γ_oil(h_3-4) – γ_mercury(h_3-2) – γ_oil(h_2-1) = P_1Let’s use the given vertical heights:- Going up 35 in. from the pipe through water (pressure decreases).
- Going down 60 in. through oil (pressure increases).
- Going up 15 in. through mercury (pressure decreases).
- Going up 40 in. through oil (pressure decreases).
P_pipe – (γ_water × 35 in) + (γ_oil × 60 in) – (γ_mercury × 15 in) – (γ_oil × 40 in) = P_1Since we need the gage pressure (P_gage = P_pipe – P_atm) and point 1 is open to the atmosphere (P_1 = P_atm), we can write the equation for gage pressure by setting P_1 to 0:
P_gage – (γ_water × 35 in) + (γ_oil × 60 in) – (γ_mercury × 15 in) – (γ_oil × 40 in) = 0 - Calculate Specific Weights (γ):
The specific weight of a fluid is its specific gravity (SG) multiplied by the specific weight of water (γ_water = 62.4 lb_f/ft³).- γ_oil = SG_oil × γ_water = 0.80 × 62.4 lb_f/ft³ = 49.92 lb_f/ft³
- γ_mercury = SG_mercury × γ_water = 13.6 × 62.4 lb_f/ft³ = 848.64 lb_f/ft³
- Solve for Gage Pressure:
Rearrange the manometer equation to solve for P_gage and convert all heights from inches to feet by dividing by 12.P_gage = (γ_water × 35/12 ft) – (γ_oil × 60/12 ft) + (γ_mercury × 15/12 ft) + (γ_oil × 40/12 ft)Now substitute the values for the specific weights:
P_gage = (62.4 × 35/12) – (49.92 × 60/12) + ( in the pipe is below atmospheric pressure (i.e., it is a vacuum or suction pressure).
