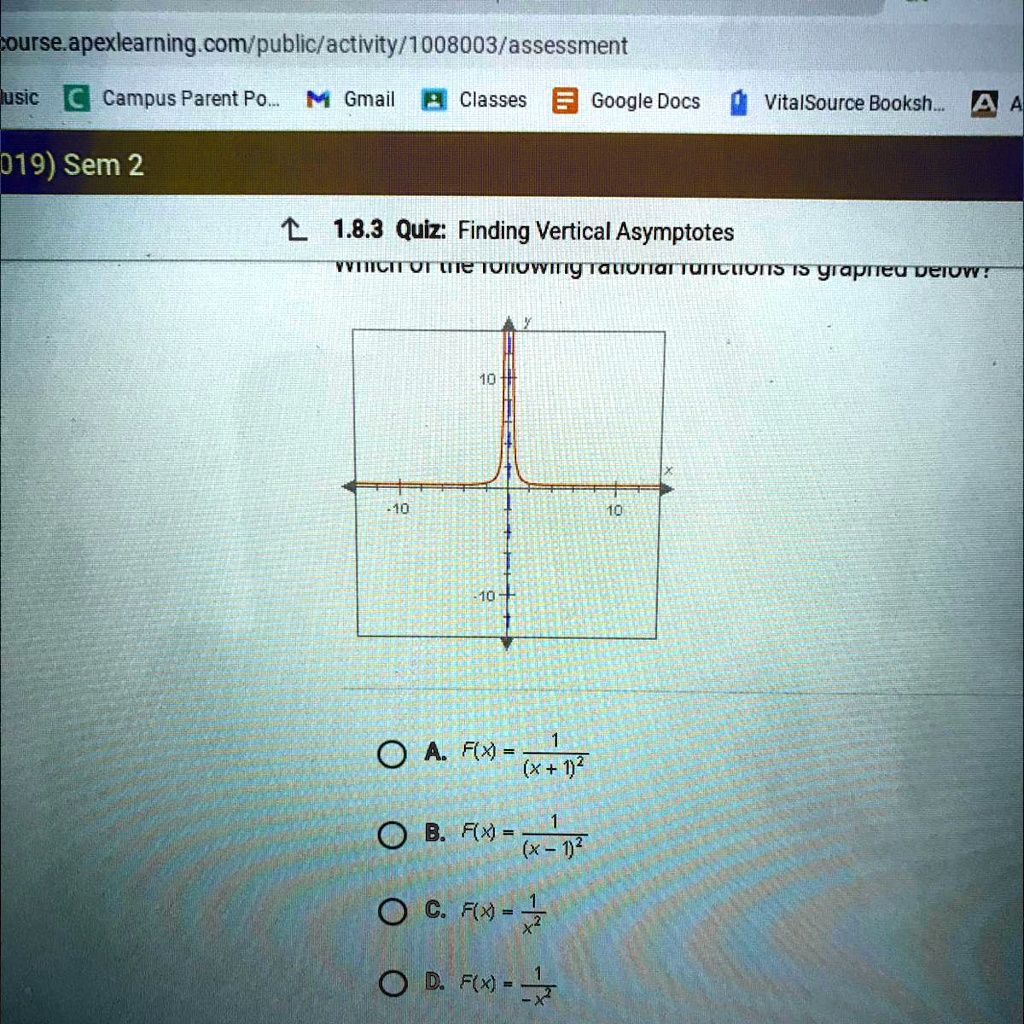
course.apexlearning.com/public/activity/1008003/assessment 019) Sem 2 ?1.8.3 Quiz: Finding Vertical Asymptotes which of the following rational functions is graphed below? -10 10 10 -10 A.
B.
C.
D.
The Correct Answer and Explanation is:
Correct Answer: C. F(x) = 1/x²
Explanation:
To determine which rational function is represented by the graph, we can analyze the key features of the graph, specifically its vertical asymptotes and its behavior around them.
1. Identifying the Vertical Asymptote:
A vertical asymptote is a vertical line that the graph of a function approaches but never touches or crosses. It occurs at x-values where the denominator of the rational function is equal to zero, provided the numerator is not also zero at that x-value.
By observing the provided graph, we can see that the function’s y-values shoot up to positive infinity as the x-values get closer and closer to 0 from both the left and the right sides. This indicates that there is a vertical asymptote at the line x = 0.
2. Evaluating the Options:
Now, let’s examine the denominator of each given function to find its vertical asymptote(s):
- A. F(x) = 1 / (x + 1)²: The denominator is zero when (x + 1)² = 0, which means x = -1. This function has a vertical asymptote at x = -1, which does not match the graph.
- B. F(x) = 1 / (x – 1)²: The denominator is zero when (x – 1)² = 0, which means x = 1. This function has a vertical asymptote at x = 1, which does not match the graph.
- C. F(x) = 1 / x²: The denominator is zero when x² = 0, which means x = 0. This function has a vertical asymptote at x = 0, which matches the graph.
- D. F(x) = -1 / x²: The denominator is zero when x² = 0, which means x = 0. This function also has a vertical asymptote at x = 0, matching the graph.
Based on the vertical asymptote, we can eliminate options A and B, leaving C and D as possibilities.
3. Analyzing the Function’s Behavior:
To choose between C and D, we look at the behavior of the graph. The entire graph lies above the x-axis, which means that the function’s values, F(x), are always positive for all x in its domain.
- For C. F(x) = 1 / x²: The numerator is 1 (a positive number). The denominator, x², is always positive for any non-zero real number x. Since a positive number divided by a positive number is always positive, F(x) will always be greater than 0. This matches the graph, where both branches go towards positive infinity.
- For D. F(x) = -1 / x²: The numerator is -1 (a negative number). The denominator, x², is always positive. A negative number divided by a positive number is always negative. This means the graph of this function would lie entirely below the x-axis. This contradicts the given graph.
Conclusion:
The function F(x) = 1/x² is the only option that has a vertical asymptote at x = 0 and produces only positive y-values, perfectly matching the provided graph.
