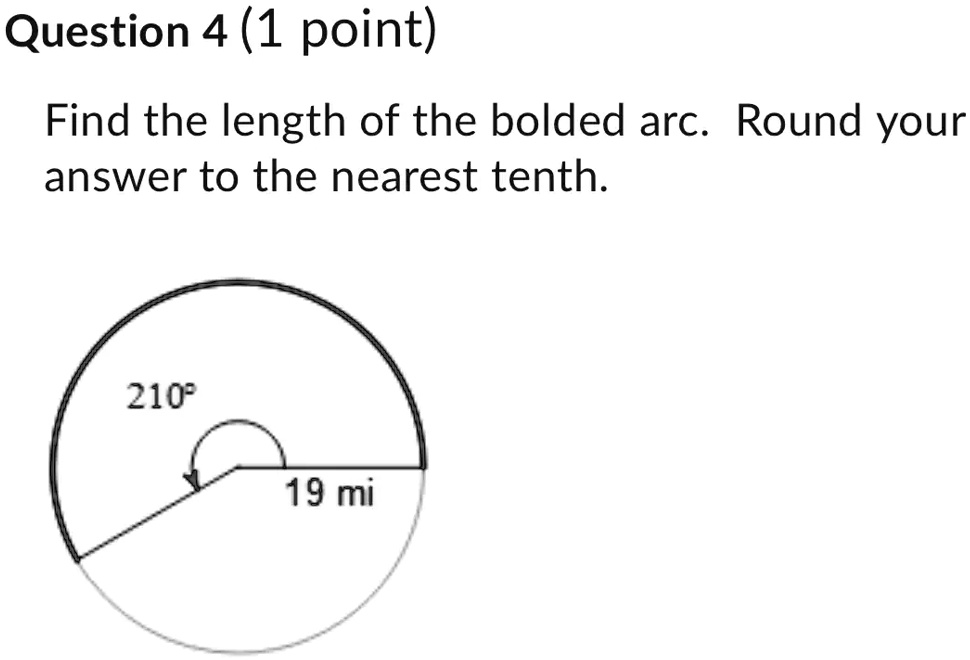
Find the length of the bolded arc. Round your answer to the nearest tenth. 210° 19 mi
The Correct Answer and Explanation is:
Of course. Here is the solution presented in a clear, step-by-step format.
Finding the Length of a Circular Arc
Objective:
To find the length of the bolded arc of a circle with a given radius and central angle. The final answer must be rounded to the nearest tenth.
Underlying Principle:
The length of a circular arc is a fraction of the total circumference of the circle. This fraction is determined by the ratio of the arc’s central angle to the total degrees in a full circle (360°). The formula for calculating the length of an arc (L) is:
L = (θ / 360°) * 2πr
where:
- θ (theta) is the central angle of the arc in degrees.
- r is the radius of the circle.
- π (pi) is a mathematical constant, approximately equal to 3.14159.
Step-by-Step Solution:
1. Identify the Given Information:
From the provided image, we extract the necessary values:
- The central angle, θ = 210°.
- The radius of the circle, r = 19 mi.
2. Substitute the Values into the Formula:
We will now substitute the identified values for θ and r into the arc length formula:
L = (210 / 360) * 2 * π * 19
3. Perform the Calculation:
First, we can simplify the fraction and the expression:
L = (210/360) * 38π
The fraction 210/360 simplifies to 21/36, which further simplifies to 7/12.
L = (7/12) * 38π
L = (266/12)π
L ≈ 22.166… * π
Now, we multiply by the value of π (≈ 3.14159):
L ≈ 22.166… * 3.14159
L ≈ 69.63864… mi
4. Round to the Nearest Tenth:
The problem asks us to round the final answer to the nearest tenth.
- The calculated length is 69.63864…
- The digit in the tenths place is 6.
- The digit immediately to its right (in the hundredths place) is 3.
Since 3 is less than 5, we keep the tenths digit as it is and drop the remaining decimal places.
Final Answer:
The length of the bolded arc is 69.6 mi.thumb_upthumb_down
