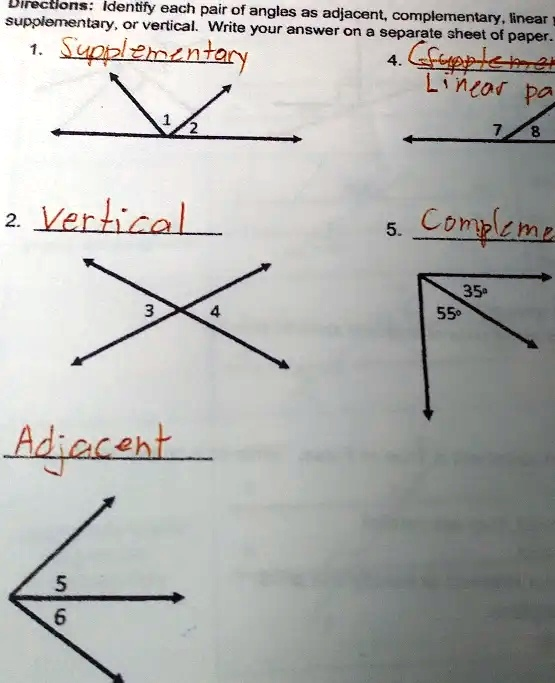
Supplementary, or vertical supplementary: Identify each pair of angles as adjacent, complementary. Write your answer on a separate sheet of paper. Supplementary not po 2 Vertical Complementary 350 550 Adjacent
The Correct Answer and Explanation is:
Of course. Here is a detailed explanation of the angle relationships presented in the worksheet, written in a clear, educational style.
Understanding Angle Pair Relationships
In geometry, the relationship between two angles is described using specific terms based on their position and the sum of their measures. Understanding these classifications is essential for solving geometric problems. The primary types of angle pairs are adjacent, vertical, complementary, and supplementary.
- Adjacent Angles: Two angles are adjacent if they share a common vertex and a common side, but have no common interior points (they don’t overlap).
- Vertical Angles: When two lines intersect, they form two pairs of opposite angles. These non-adjacent, opposite angles are called vertical angles. A key property is that vertical angles are always equal in measure.
- Complementary Angles: Two angles are complementary if the sum of their measures is 90 degrees. They can be adjacent (forming a right angle) or non-adjacent.
- Supplementary Angles: Two angles are supplementary if the sum of their measures is 180 degrees.
- Linear Pair: This is a special case where two adjacent angles have non-common sides that form a straight line. A linear pair is always supplementary.
Analysis of the Problems
1. Angles 1 and 2:
These two angles share a common vertex and a common side, which makes them adjacent. Their non-common sides form a straight line. This specific arrangement is known as a linear pair. Because they form a linear pair, their measures add up to 180°, making them supplementary. Therefore, the most accurate descriptions are linear pair and supplementary.
2. Angles 3 and 4:
These angles are formed by two intersecting lines and are directly opposite each other. They do not share a common side. This is the definition of vertical angles. Vertical angles are always congruent (equal in measure).
3. Angles 5 and 6:
These angles share a common vertex and a common side, with no overlapping interior points. This fits the definition of adjacent angles. Without any given measures or symbols indicating a right angle or straight line, this is the most precise classification we can make.
4. Angles 7 and 8:
Similar to the first problem, angles 7 and 8 are adjacent as they share a vertex and a side. Their outer rays form a straight line, making them a linear pair. Consequently, they are also supplementary because their measures sum to 180°.
5. Angles measuring 35° and 55°:
To classify this pair, we must use their given measures. By adding them together (35° + 55° = 90°), we find that their sum is 90 degrees. By definition, two angles whose measures sum to 90° are complementary angles. In this diagram, they are also adjacent.
