Work out the value of n
when n = 5(2k² + 3k – 6),
and k=-2
.
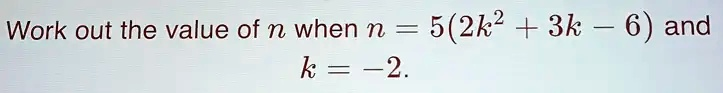
The Correct Answer and Explanation is:
The value of n is -20.
To determine the value of n, the given value for k must be substituted into the equation. The equation provided is n = 5(2k² + 3k – 6), and the value for k is -2.
The first step is to replace every instance of ‘k’ in the equation with the value -2:
n = 5(2(-2)² + 3(-2) – 6)
Following the order of operations (PEMDAS/BODMAS), the calculations inside the parentheses are performed first. Within the parentheses, exponents are handled before multiplication, addition, or subtraction.
- Calculate the exponent: The term (-2)² means -2 multiplied by -2, which equals 4.
The equation now becomes: n = 5(2(4) + 3(-2) – 6) - Perform multiplication within the parentheses:
- Multiply 2 by 4 to get 8.
- Multiply 3 by -2 to get -6.
The equation is now simplified to: n = 5(8 – 6 – 6)
- Perform addition and subtraction within the parentheses: Working from left to right, first subtract 6 from 8, which results in 2. Then, subtract the remaining 6 from 2.
- 8 – 6 = 2
- 2 – 6 = -4
The expression inside the parentheses simplifies to -4. The equation is now: n = 5(-4)
- Perform the final multiplication: The last step is to multiply 5 by the result from the parentheses, which is -4.
5 × -4 = -20
Therefore, when k = -2, the value of n is -20.
