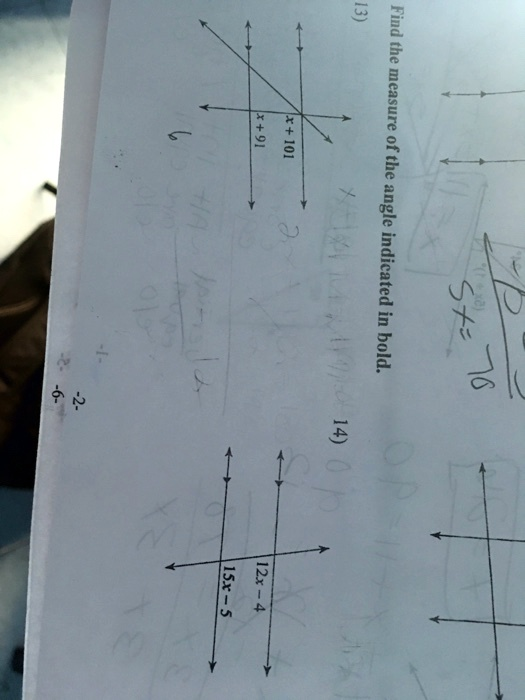
Find the measure of the angle indicated in bold. 13) x + 101 16 + x 14) 12x – 4 15x – 5
The Correct Answer and Explanation is:
Based on the images provided, here are the solutions to the geometry problems.
Problem 13
The angle indicated in bold is the one with the expression x + 101.
Answer: The measure of the angle is 95 degrees.
Explanation:
In this diagram, two angles, labeled with the expressions x + 101 and x + 91, are adjacent to each other on a straight line. Angles that form a straight line are known as a linear pair, and their measures are supplementary, meaning they add up to 180 degrees.
To find the value of x, an equation can be set up by adding the two expressions and setting the sum equal to 180:
(x + 101) + (x + 91) = 180
First, combine the like terms on the left side of the equation:
2x + 192 = 180
Next, isolate the term with x by subtracting 192 from both sides of the equation:
2x = 180 – 192
2x = -12
Finally, solve for x by dividing both sides by 2:
x = -6
Now that the value of x is known, it can be substituted back into the expression for the bolded angle, x + 101:
Measure = (-6) + 101
Measure = 95
Therefore, the measure of the angle indicated in bold is 95 degrees. The other angle would be (-6) + 91 = 85 degrees. As a check, 95 + 85 = 180, which confirms the calculations are correct.
Problem 14
The angle indicated in bold is the one with the expression 15x – 5.
Answer: The measure of the angle is 100 degrees.
Explanation:
This problem shows two parallel lines intersected by a transversal line. The two angles, labeled 12x – 4 and 15x – 5, are located between the parallel lines and on the same side of the transversal. This relationship identifies them as consecutive interior angles (or same-side interior angles). A property of parallel lines states that consecutive interior angles are supplementary, so their measures sum to 180 degrees.
This relationship allows for the creation of the following equation:
(12x – 4) + (15x – 5) = 180
Begin by combining the like terms on the left side:
27x – 9 = 180
To solve for x, first add 9 to both sides of the equation:
27x = 189
Then, divide both sides by 27 to find the value of x:
x = 7
With the value of x determined, substitute it into the expression for the bolded angle, 15x – 5:
Measure = 15(7) – 5
Measure = 105 – 5
Measure = 100
The measure of the angle indicated in bold is 100 degrees. The other angle’s measure is 12(7) – 4 = 84 – 4 = 80 degrees. The sum of these two angles is 100 + 80 = 180, which validates the supplementary relationship and the final answer.thumb_upthumb_down
