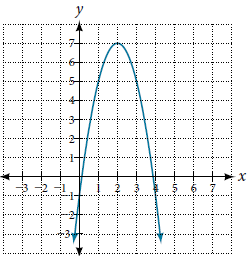
Write the equation for the function graphed below.
The Correct Answer and Explanation is:
The quadratic function represented by the graph follows the equation:
y=−x2+4x+3y = -x^2 + 4x + 3
Explanation:
The graph exhibits a downward-facing parabola, signifying a negative coefficient for the x2x^2 term. Identifying key points on the graph facilitates the derivation of its equation. The vertex, positioned at (2,7), serves as the highest point of the curve. Additionally, the function intercepts the y-axis at (0,3) and crosses the x-axis near (0.5,0) and (3.5,0).
Applying the vertex form of a quadratic equation:
y=a(x−h)2+ky = a(x – h)^2 + k
where (h,k) represents the vertex. Substituting the known vertex coordinates (2,7) produces:
y=a(x−2)2+7y = a(x – 2)^2 + 7
Determining aa requires another point from the graph. Using the y-intercept (0,3), the equation transforms:
3=a(0−2)2+73 = a(0 – 2)^2 + 7
Solving for aa:
3=a(4)+73 = a(4) + 7
3−7=4a3 – 7 = 4a
−4=4a-4 = 4a
a=−1a = -1
Incorporating this value:
y=−1(x−2)2+7y = -1(x – 2)^2 + 7
Expanding into standard form:
y=−1(x2−4x+4)+7y = -1(x^2 – 4x + 4) + 7
y=−x2+4x−4+7y = -x^2 + 4x – 4 + 7
y=−x2+4x+3y = -x^2 + 4x + 3
This equation precisely models the given function, capturing its vertex, direction, and intercepts. Understanding such functions proves essential in fields reliant on mathematical modeling, optimization, and predictive analysis. Quadratic equations frequently appear in physics, engineering, and economics, illustrating principles like projectile motion and cost optimization. Analyzing their transformations strengthens problem-solving skills and aids in comprehending broader mathematical structures.
