Akite that is not a parallelogram
The Correct Answer and Explanation is:
Correct Answer:
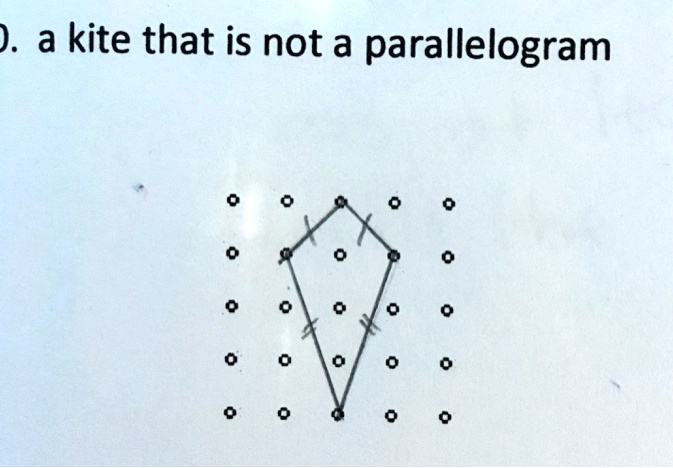
The shape shown is a kite that is not a parallelogram.
Explanation
The figure represents a quadrilateral with two distinct pairs of adjacent sides that are equal in length. The top two sides are congruent, and the bottom two sides are also congruent, but the lengths of the top and bottom pairs are not the same. This creates a kite shape, which satisfies the formal definition of a kite in geometry.
A kite is a type of quadrilateral characterized by having two pairs of adjacent sides that are congruent. These pairs share a common vertex, forming a symmetrical shape with reflectional symmetry across one diagonal. In contrast, a parallelogram requires both pairs of opposite sides to be equal in length and parallel, which this shape does not have.
In the image, the opposite sides are clearly not equal. The top and bottom segments differ in length, and the sides do not run parallel to each other. The lack of parallel opposite sides disqualifies the shape from being a parallelogram. Additionally, parallelograms exhibit rotational symmetry of 180 degrees, which this shape does not possess.
The kite’s diagonals have a unique relationship: one diagonal (typically the longer one) bisects the other at a right angle. This is not shown explicitly in the image but is a known property of kites. This right-angle intersection of diagonals is another property that differentiates kites from general parallelograms, whose diagonals bisect each other but are not necessarily perpendicular.
This figure matches the textbook geometric definition of a kite and simultaneously violates the conditions for a parallelogram. As such, it serves as a clear and accurate example of a kite that is not a parallelogram, showcasing the important distinctions between these two types of quadrilaterals.
