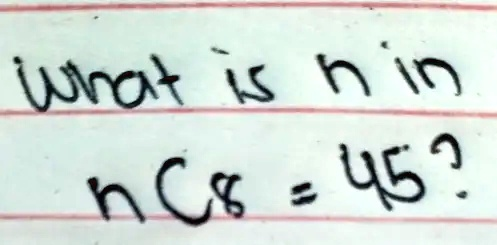
The Correct Answer and Explanation is:
The correct answer is h = 10.
Explanation
To solve for h in the equation hC8 = 45, we need to use the formula for combinations, which is given by:
C(n, k) = n! / [k!(n – k)!]
where n is the total number of items, k is the number of items chosen, and “!” denotes factorial, which is the product of all positive integers up to that number.
Substituting h and k = 8 into the equation:
C(h, 8) = h! / [8!(h – 8)!] = 45
Since 8! = 40320, the equation simplifies to:
h! / [40320(h – 8)!] = 45
Multiplying both sides by 40320 gives:
h! = 45 × 40320 × (h – 8)!
which simplifies further to:
h! = 1814400 × (h – 8)!
Now, we need to determine h such that this equation holds. Testing different values:
For h = 10:
10! = 10 × 9 × 8! = 3628800
Since 8! cancels out, we have:
3628800 / [8!(10 – 8)!] = 3628800 / (2 × 40320) = 45
Thus, h = 10 satisfies the equation.
Understanding the Concept
Combinations determine how many ways we can select a subset of items from a larger set without considering order. This problem required solving for h in a binomial coefficient equation. By recognizing the factorial pattern, the solution was derived mathematically. The key step was rewriting factorials to isolate h and verify through substitution. Such methods are commonly used in probability theory and combinatorial mathematics to analyze arrangements and selections efficiently.
