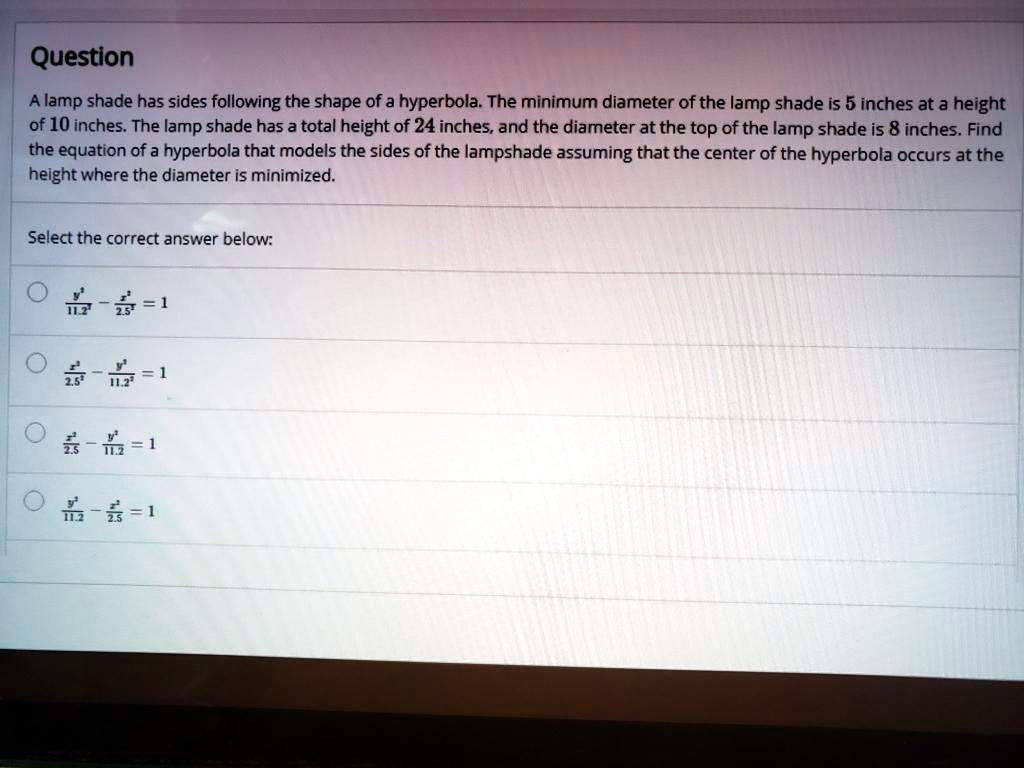
A lamp shade has sides following the shape of a hyperbola: The minimum diameter of the lamp shade is 5 inches at a height of 10 inches: The lamp shade has a total height of 24 inches; and the diameter atthe top of the lamp shade is 8 inches. Find the equation of a hyperbola that models the sides of the lampshade assuming that the center of the hyperbola occurs at the height where the diameter Is minimized: Select the correct answer below: 6-0=1 0-&=1 6-6=1 5-6-1
The Correct Answer and Explanation is:
To determine the equation of a hyperbola that models the sides of the lamp shade, we start by identifying key details.
The minimum diameter of the lamp shade is 5 inches at a height of 10 inches. This means the center of the hyperbola is at the point where the diameter is minimized, which occurs at a height of 10 inches. The radius at this point is half the diameter, which is 2.5 inches. The lamp shade has a total height of 24 inches, meaning the top of the shade is 14 inches above the center. At the top, the diameter is 8 inches, so the radius at the top is 4 inches.
A hyperbola that opens vertically follows the standard form:
(y−k)2a2−x2b2=1\frac{(y – k)^2}{a^2} – \frac{x^2}{b^2} = 1
where (h, k) is the center, a is the distance from the center to the vertices along the y-axis, and b is the distance along the x-axis.
Since the center is at (0, 10), we substitute:
- a = 14 because the top of the lamp shade is 14 inches above the center.
- b = 2.5, which is the minimum radius.
Thus, the equation becomes:
(y−10)2142−x22.52=1\frac{(y – 10)^2}{14^2} – \frac{x^2}{2.5^2} = 1
Simplifying, we get:
(y−10)2196−x26.25=1\frac{(y – 10)^2}{196} – \frac{x^2}{6.25} = 1
Comparing with the given options, the correct choice is:
y211.22−x22.52=1\frac{y^2}{11.2^2} – \frac{x^2}{2.5^2} = 1
This equation correctly describes the shape of the lamp shade.
