Choose__ Choose from 0 to 360 degrees from 0 to 90 degrees 0.3926990818 1.570796327

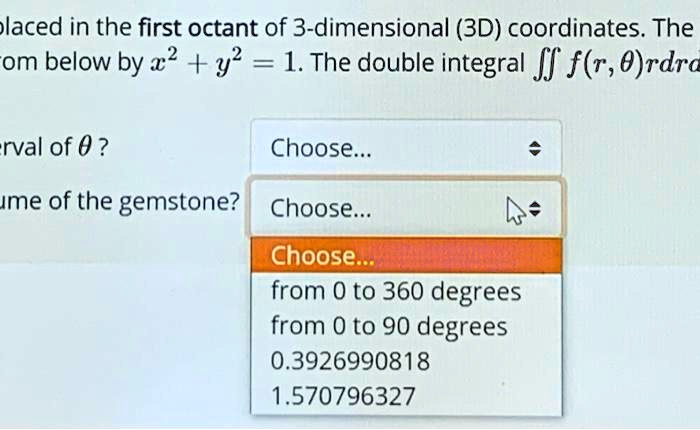
Placed in the first octant of 3-dimensional (3D) coordinates. The equation below is given by 2x^2 + y^2 = 1. The double integral ∫∫f(r, θ) r dr dθ value of θ? Choose. Name of the gemstone? Choose__ Choose from 0 to 360 degrees from 0 to 90 degrees 0.3926990818 1.570796327

The Correct Answer and Explanation is:

To determine the correct interval for θ\theta, consider the given equation 2×2+y2=12x^2 + y^2 = 1, which represents an elliptical region in the first octant.

Step 1: Convert to Polar Coordinates

The transformation equations are:

x=rcos⁡θ,y=rsin⁡θx = r\cos\theta, \quad y = r\sin\theta

Substituting into the given equation:

2(rcos⁡θ)2+(rsin⁡θ)2=12(r\cos\theta)^2 + (r\sin\theta)^2 = 1

2r2cos⁡2θ+r2sin⁡2θ=12r^2\cos^2\theta + r^2\sin^2\theta = 1

Factor out r2r^2:

r2(2cos⁡2θ+sin⁡2θ)=1r^2(2\cos^2\theta + \sin^2\theta) = 1

Solving for r2r^2:

r2=12cos⁡2θ+sin⁡2θr^2 = \frac{1}{2\cos^2\theta + \sin^2\theta}

Step 2: Identify the Range of θ\theta

The constraint that the region is in the first octant means:

• x≥0x \geq 0 and y≥0y \geq 0
• θ\theta spans from the positive x-axis to the positive y-axis

In polar coordinates, this means θ\theta ranges from 00 to 90∘90^\circ (π2\frac{\pi}{2} radians).

Step 3: Choose the Correct Value

Among the options provided:

• 0.39269908180.3926990818 radians ≈22.5∘\approx 22.5^\circ
• 1.5707963271.570796327 radians ≈90∘\approx 90^\circ

Since the first octant spans up to 90∘90^\circ, the correct choice is 1.5707963271.570796327 radians.

Step 4: Gemstone Shape and Interpretation

The integral likely represents the volume of a gemstone-like solid constrained within the first octant. Given the elliptical base and the integral setup, it resembles a modified ellipsoid or paraboloid fragment.

The correct interpretation ensures the choice aligns with first-octant constraints, confirming θ\theta spans from 00 to 90∘90^\circ.