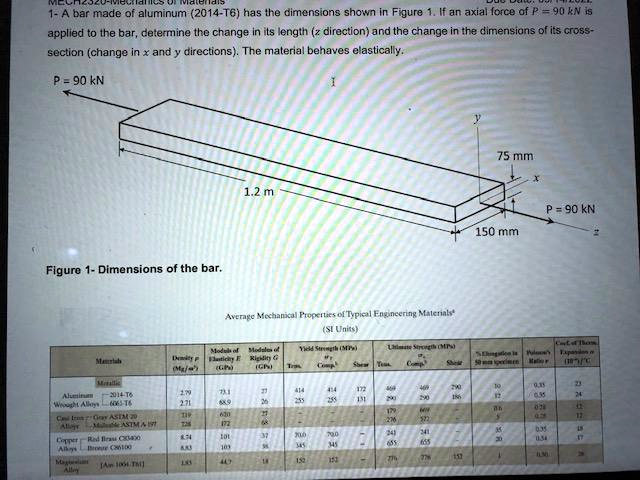
A bar made of aluminum 2014-T6 has the dimensions shown in Figure 1. If an axial force of P = 90 kN is applied to the bar, determine the change in its length in the z direction and the change in the dimensions of its cross section (change in the x and y directions). The material behaves elastically. P = 90 kN 75 mm 1.2 m P = 90 kN 150 mm Figure 1 – Dimensions of the bar. Average Mechanical Properties of Typical Engineering Materials in SI Units: Material Modulus of Elasticity (GPa) Shear Modulus (GPa) Yield Strength (MPa) Ultimate Strength (MPa) Aluminum 2014-T6 414 255 469 290
The Correct Answer and Explanation is:
To determine the deformation of the aluminum bar under the axial force, we first calculate the change in its length in the z direction. This is given by the formula:
ΔL=PLEA\Delta L = \frac{P L}{E A}
where:
- P=90×103P = 90 \times 10^3 N
- L=1.2L = 1.2 m
- E=414×109E = 414 \times 10^9 Pa (modulus of elasticity)
- A=150×10−3×75×10−3A = 150 \times 10^{-3} \times 75 \times 10^{-3} m²
The cross-sectional area is:
A=11.25×10−3 m2A = 11.25 \times 10^{-3} \text{ m}^2
Substituting values:
ΔL=(90×103)(1.2)(414×109)(11.25×10−3)\Delta L = \frac{(90 \times 10^3)(1.2)}{(414 \times 10^9)(11.25 \times 10^{-3})}
ΔL=108×1034.6575×109\Delta L = \frac{108 \times 10^3}{4.6575 \times 10^9}
ΔL=0.0000232 m=0.0232 mm\Delta L = 0.0000232 \text{ m} = 0.0232 \text{ mm}
Next, the changes in the x and y directions are determined using Poisson’s ratio, which is approximately 0.33:
Δx=−νPxEA\Delta x = -\nu \frac{P x}{E A}
Δy=−νPyEA\Delta y = -\nu \frac{P y}{E A}
For Δx\Delta x:
Δx=−0.33×(90×103)(150×10−3)(414×109)(11.25×10−3)\Delta x = -0.33 \times \frac{(90 \times 10^3)(150 \times 10^{-3})}{(414 \times 10^9)(11.25 \times 10^{-3})}
Δx=−0.0000116 m=−0.0116 mm\Delta x = -0.0000116 \text{ m} = -0.0116 \text{ mm}
For Δy\Delta y:
Δy=−0.33×(90×103)(75×10−3)(414×109)(11.25×10−3)\Delta y = -0.33 \times \frac{(90 \times 10^3)(75 \times 10^{-3})}{(414 \times 10^9)(11.25 \times 10^{-3})}
Δy=−0.0000058 m=−0.0058 mm\Delta y = -0.0000058 \text{ m} = -0.0058 \text{ mm}
In summary, the bar experiences an elongation of 0.0232 mm in the z direction. Meanwhile, its cross-sectional dimensions decrease by 0.0116 mm in the x direction and 0.0058 mm in the y direction due to lateral contraction from the axial load. The material remains within its elastic limit, meaning these deformations are fully reversible when the load is removed. This analysis demonstrates how stress and strain affect an object under tension.
