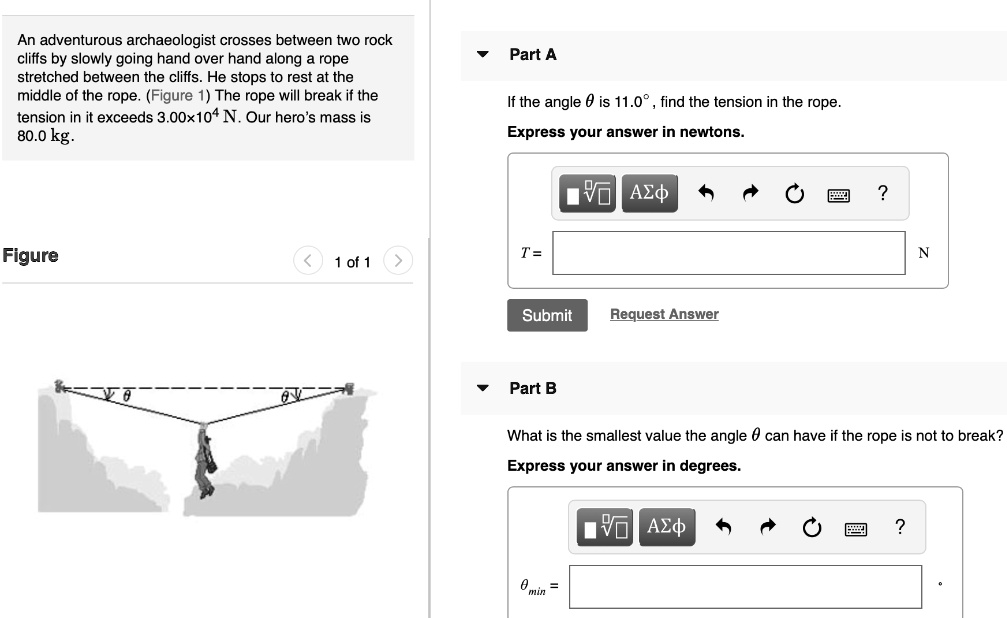
An adventurous archaeologist crosses between two rock cliffs by slowly going hand over hand along a rope stretched between the cliffs. He stops to rest at the middle of the rope. (Figure 1) The rope will break if the tension in it exceeds 3.00×10^4 N. Our hero’s mass is 80.0 kg. Part A If the angle
is 11.0°, find the tension in the rope. Express your answer in newtons. Figure T= < 1 of 1 > ? ??? Submit Request Answer Part B ? N What is the smallest value the angle
can have if the rope is not to break? Express your answer in degrees. ? ???
The Correct Answer and Explanation is:
Part A: Finding the Tension in the Rope at 11.0°
Given:
- Mass of the archaeologist: m=80.0 kgm = 80.0 \, \text{kg}m=80.0kg
- Angle between rope and horizontal: θ=11.0∘\theta = 11.0^\circθ=11.0∘
- Gravitational acceleration: g=9.8 m/s2g = 9.8 \, \text{m/s}^2g=9.8m/s2
The vertical forces must balance the weight:2Tsin(θ)=mg2T\sin(\theta) = mg2Tsin(θ)=mg
Solving for TTT:T=mg2sin(θ)T = \frac{mg}{2\sin(\theta)}T=2sin(θ)mg
Substitute the values:T=(80.0)(9.8)2sin(11.0∘)T = \frac{(80.0)(9.8)}{2\sin(11.0^\circ)}T=2sin(11.0∘)(80.0)(9.8)T=7842×0.1908=7840.3816≈2054.6 NT = \frac{784}{2 \times 0.1908} = \frac{784}{0.3816} \approx 2054.6 \, \text{N}T=2×0.1908784=0.3816784≈2054.6N
Answer for Part A:T≈2.05×103 NT \approx 2.05 \times 10^3 \, \text{N}T≈2.05×103N
Part B: Smallest Angle to Avoid Rope Breakage
The maximum tension before the rope breaks is Tmax=3.00×104 NT_{\text{max}} = 3.00 \times 10^4 \, \text{N}Tmax=3.00×104N. Use the same equation:2Tsin(θ)=mg2T\sin(\theta) = mg2Tsin(θ)=mg
Solving for sin(θ)\sin(\theta)sin(θ):sin(θ)=mg2T=(80.0)(9.8)2(3.00×104)=78460000≈0.01307\sin(\theta) = \frac{mg}{2T} = \frac{(80.0)(9.8)}{2(3.00 \times 10^4)} = \frac{784}{60000} \approx 0.01307sin(θ)=2Tmg=2(3.00×104)(80.0)(9.8)=60000784≈0.01307
Now find θ\thetaθ:θ=arcsin(0.01307)≈0.75∘\theta = \arcsin(0.01307) \approx 0.75^\circθ=arcsin(0.01307)≈0.75∘
Answer for Part B:θmin≈0.75∘\theta_{\text{min}} \approx 0.75^\circθmin≈0.75∘
Explanation
In this problem, a person is hanging at the center of a horizontal rope stretched between two cliffs. The tension in the rope increases as the angle between the rope and the horizontal becomes smaller. This is because a smaller angle causes the vertical component of the tension to be less effective in supporting the person’s weight. The vertical force must match the weight of the person, which is mgmgmg, where mmm is mass and ggg is the gravitational constant.
Since there are two symmetrical rope segments supporting the person, each side carries half of the vertical load. We use the equation 2Tsin(θ)=mg2T\sin(\theta) = mg2Tsin(θ)=mg, which balances the upward components of the tension with the downward force of gravity.
In part A, when the angle is 11 degrees, we calculate the total tension by solving for TTT from the above equation. Plugging in the numbers, we get about 2054.6 newtons, which is well within the maximum allowed tension of the rope.
In part B, we are asked to find the smallest angle before the rope breaks. This means the tension reaches the limit of 30000 newtons. Using the same equation but solving for θ\thetaθ, we first find the sine of the angle and then use the inverse sine function to determine the angle. The result is approximately 0.75 degrees, showing that if the rope dips below this angle, it will snap under the person’s weight.
