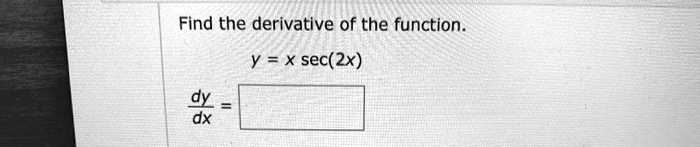
Find the derivative of the function. y = x sec(2x) \frac{dy}{dx} =
The Correct Answer and Explanation is:
To differentiate the function y=x⋅sec(2x)y = x \cdot \sec(2x)y=x⋅sec(2x), we need to apply both the product rule and the chain rule.
Step 1: Apply the product rule
The product rule states that if y=u⋅vy = u \cdot vy=u⋅v, then:dydx=u′⋅v+u⋅v′\frac{dy}{dx} = u’ \cdot v + u \cdot v’dxdy=u′⋅v+u⋅v′
Here, u=xu = xu=x and v=sec(2x)v = \sec(2x)v=sec(2x). We need to find the derivatives of uuu and vvv.
- The derivative of u=xu = xu=x is u′=1u’ = 1u′=1.
- The derivative of v=sec(2x)v = \sec(2x)v=sec(2x) requires the chain rule.
Step 2: Apply the chain rule to v=sec(2x)v = \sec(2x)v=sec(2x)
The chain rule states that the derivative of a composite function f(g(x))f(g(x))f(g(x)) is:ddx[f(g(x))]=f′(g(x))⋅g′(x)\frac{d}{dx} [f(g(x))] = f'(g(x)) \cdot g'(x)dxd[f(g(x))]=f′(g(x))⋅g′(x)
In this case, f(x)=sec(x)f(x) = \sec(x)f(x)=sec(x), and the derivative of sec(x)\sec(x)sec(x) is sec(x)tan(x)\sec(x) \tan(x)sec(x)tan(x). So, applying the chain rule:ddx[sec(2x)]=sec(2x)⋅tan(2x)⋅ddx[2x]=2⋅sec(2x)⋅tan(2x)\frac{d}{dx} [\sec(2x)] = \sec(2x) \cdot \tan(2x) \cdot \frac{d}{dx}[2x] = 2 \cdot \sec(2x) \cdot \tan(2x)dxd[sec(2x)]=sec(2x)⋅tan(2x)⋅dxd[2x]=2⋅sec(2x)⋅tan(2x)
Step 3: Combine the results using the product rule
Now, substitute everything back into the product rule:dydx=1⋅sec(2x)+x⋅(2⋅sec(2x)⋅tan(2x))\frac{dy}{dx} = 1 \cdot \sec(2x) + x \cdot \left( 2 \cdot \sec(2x) \cdot \tan(2x) \right)dxdy=1⋅sec(2x)+x⋅(2⋅sec(2x)⋅tan(2x))
Thus, the derivative is:dydx=sec(2x)+2x⋅sec(2x)⋅tan(2x)\frac{dy}{dx} = \sec(2x) + 2x \cdot \sec(2x) \cdot \tan(2x)dxdy=sec(2x)+2x⋅sec(2x)⋅tan(2x)
Conclusion:
The derivative of the function y=x⋅sec(2x)y = x \cdot \sec(2x)y=x⋅sec(2x) is:dydx=sec(2x)+2x⋅sec(2x)⋅tan(2x)\frac{dy}{dx} = \sec(2x) + 2x \cdot \sec(2x) \cdot \tan(2x)dxdy=sec(2x)+2x⋅sec(2x)⋅tan(2x)
