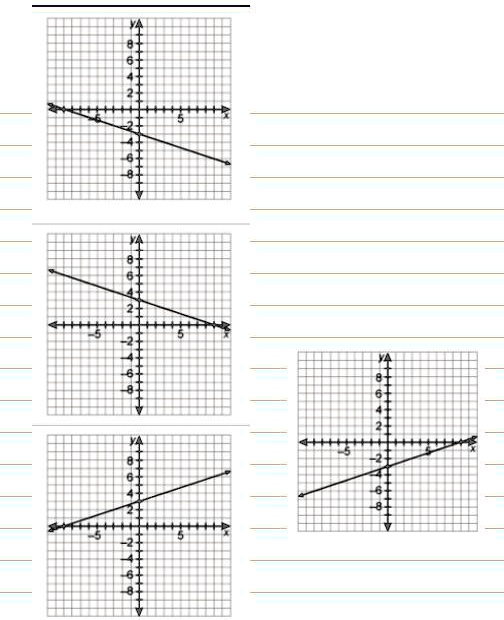
The Correct Answer and Explanation is:
Here are the equations for each of the four graphed lines:
- Top Left Graph: y = -1/2x – 2
- Middle Left Graph: y = -1/2x + 2
- Bottom Left Graph: y = 1/2x + 2
- Middle Right Graph: y = 1/2x – 2
To determine the equation for each line, we use the slope-intercept form, which is written as y = mx + b. In this formula, ‘b’ represents the y-intercept, which is the point where the line crosses the vertical y-axis. The variable ‘m’ represents the slope of the line, which measures its steepness and direction. The slope is calculated as “rise over run,” or the change in the vertical position (y) divided by the change in the horizontal position (x) between any two points on the line.
For the top left graph, the line intersects the y-axis at -2, so the y-intercept (b) is -2. To find the slope (m), we can select two clear points on the line, such as the y-intercept (0, -2) and another point, (4, -4). The vertical change, or rise, is from -2 to -4, which is a change of -2. The horizontal change, or run, is from 0 to 4, which is a change of +4. Therefore, the slope (m) is -2/4, which simplifies to -1/2. The line slopes downward from left to right, confirming the negative slope. The final equation is y = -1/2x – 2.
For the middle left graph, the line crosses the y-axis at +2, making the y-intercept (b) equal to 2. Using the y-intercept (0, 2) and another point on the line, (4, 0), we can calculate the slope. The rise is from 2 to 0, a change of -2, and the run is from 0 to 4, a change of +4. The slope (m) is -2/4, which simplifies to -1/2. The equation for this line is y = -1/2x + 2.
For the bottom left graph, the line’s y-intercept (b) is also at +2. This line, however, slopes upward from left to right, indicating a positive slope. Using the points (0, 2) and (4, 4), we see the rise is from 2 to 4, which is +2, and the run is from 0 to 4, which is +4. The slope (m) is 2/4, or 1/2. The resulting equation is y = 1/2x + 2.
Finally, for the middle right graph, the line intersects the y-axis at -2, so b = -2. This line also slopes upward, so we expect a positive slope. Let’s use the points (0, -2) and (4, 0). The rise is from -2 to 0 (+2), and the run is from 0 to 4 (+4). The slope (m) is 2/4, which simplifies to 1/2. Thus, the equation for this line is y = 1/2x – 2. By systematically identifying the y-intercept and calculating the slope for each line, we can accurately determine its unique linear equation
