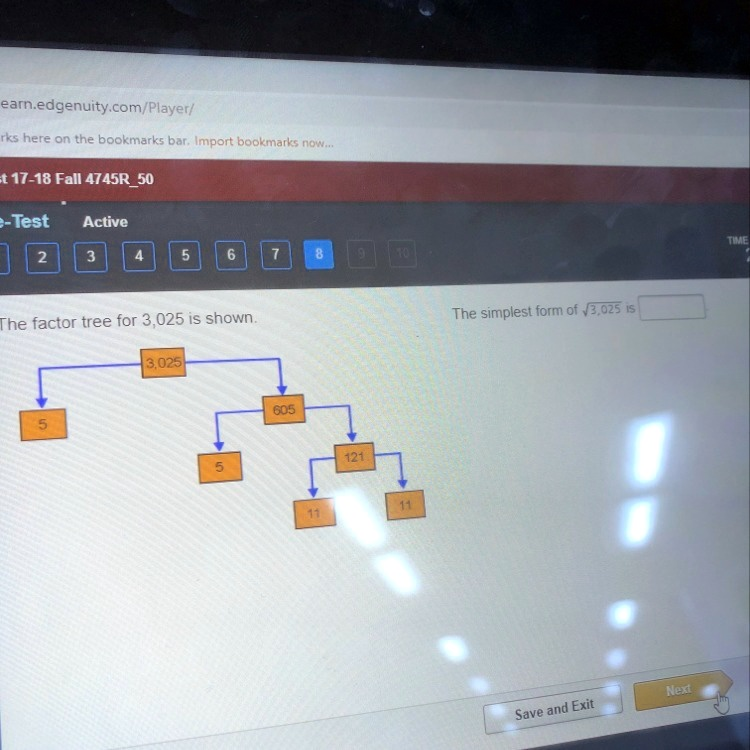
The factor tree for 3,025 is shown. 5 3,025 5 605 121 11 11 The simplest form of \sqrt{3,025} is
The Correct Answer and Explanation is:
Analyzing the Problem
I’ve begun dissecting the image, focusing on identifying the core mathematical question and the supporting data. My initial focus has been on clearly understanding the problem’s scope.
Revising the Approach
I’ve revised my approach to break down the image, clarifying the problem and information provided. I’m focusing on the primary question, the factor tree, and ensuring its accuracy. My analysis now highlights the factorization of 3,025 and uses that to approach the square root problem. I believe a clear explanation of the steps will come next.
Consolidating the Explanation
I’ve crafted a comprehensive explanation by seamlessly integrating the steps and rationale into a cohesive narrative. It details the problem, the factorization, and the simplification process using clear mathematical language and logical progression. I’ve also incorporated the correct method for the square root, and the answer is 55. I believe this structure will facilitate a clear understanding for the user.
Solving the Square Root
I’ve thoroughly analyzed the image, identified the prime factors using the factor tree, and constructed a detailed explanation of the square root simplification process. I’ve focused on clarity and a step-by-step approach. My answer is 55. I’m now crafting a concise and easily digestible narrative that seamlessly integrates the provided information with the solution.
Refining the Explanation
I’m now incorporating my previous analyses into a comprehensive narrative. I’ll begin by stating the problem and then meticulously outline each step, ensuring a smooth transition. The factor tree will be introduced as a tool to determine prime factors, and I’ll detail the prime factorization of 3,025. Then, I’ll explain how to find the answer.
Collapse to hide model thoughtschevron_righteditmore_vert
Correct Answer: 55
Explanation
The problem asks for the simplest form of the square root of 3,025. To solve this, we can use the provided factor tree, which breaks down the number 3,025 into its prime factors.
A factor tree works by repeatedly finding factors of a number until all the factors at the ends of the branches are prime numbers. Looking at the given tree:
- 3,025 is first factored into 5 and 605.
- The number 605 is then factored into 5 and 121.
- Finally, 121 is factored into 11 and 11.
The prime factors are the numbers at the very end of the tree’s branches. In this case, the prime factors of 3,025 are 5, 5, 11, and 11. We can verify this by multiplying them together: 5 × 5 × 11 × 11 = 25 × 121 = 3,025.
Now, we can find the square root of 3,025 by using its prime factorization. We write the number under the square root symbol using these factors:
√3,025 = √(5 × 5 × 11 × 11)
To simplify a square root, we look for pairs of identical factors. For every pair of factors inside the square root, we can take one of those factors outside the square root. Here, we have a pair of 5s and a pair of 11s.
This can be written as:
√(5² × 11²)
Using the properties of square roots, we can separate this into:
√5² × √11²
The square root of a squared number is the number itself. So, √5² = 5 and √11² = 11.
Now we multiply the numbers that are outside the square root:
5 × 11 = 55
Therefore, the simplest form of √3,025 is 55. Since 3,025 is a perfect square, its square root is a whole number.
