The Correct Answer and Explanation is:
The correct answer is 55.
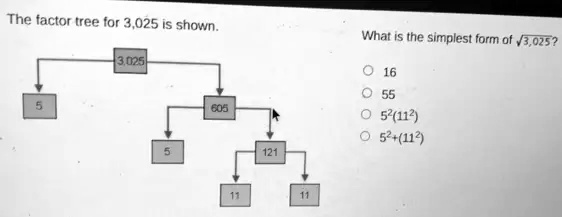
This problem asks for the simplest form of the square root of 3,025. The provided factor tree is a visual tool designed to help break down the number 3,025 into its prime factors. Prime factors are the prime numbers that multiply together to create the original number.
First, let’s interpret the factor tree. The tree begins with 3,025 at the top. It branches out to show that 3,025 can be factored into 5 and 605. The number 605 is then factored further into 5 and 121. Finally, 121 is factored into 11 and 11. The numbers at the end of the branches (5, 5, 11, and 11) are the prime factors of 3,025 because they cannot be factored any further.
From this information, we can write the prime factorization of 3,025 as the product of these numbers:
3,025 = 5 × 5 × 11 × 11
To make simplifying the square root easier, we can express this factorization using exponents. Since we have two factors of 5 and two factors of 11, we can write this as:
3,025 = 5² × 11²
Now, we can find the square root of 3,025 by taking the square root of its prime factorization:
√3,025 = √(5² × 11²)
A key property of square roots allows us to split the root of a product into the product of the roots:
√(5² × 11²) = √5² × √11²
The square root function is the inverse operation of squaring a number. This means that the square root of a number squared is the number itself. Therefore, √5² simplifies to 5, and √11² simplifies to 11.
The final step is to multiply these resulting numbers:
5 × 11 = 55
Thus, the simplest form of √3,025 is 55. Reviewing the other choices confirms this. Option 16 is incorrect because 16² = 256. Option 5²(11²) is another way of writing 3,025, not its square root. Option 5²+(11²) is an addition expression that equals 146.
