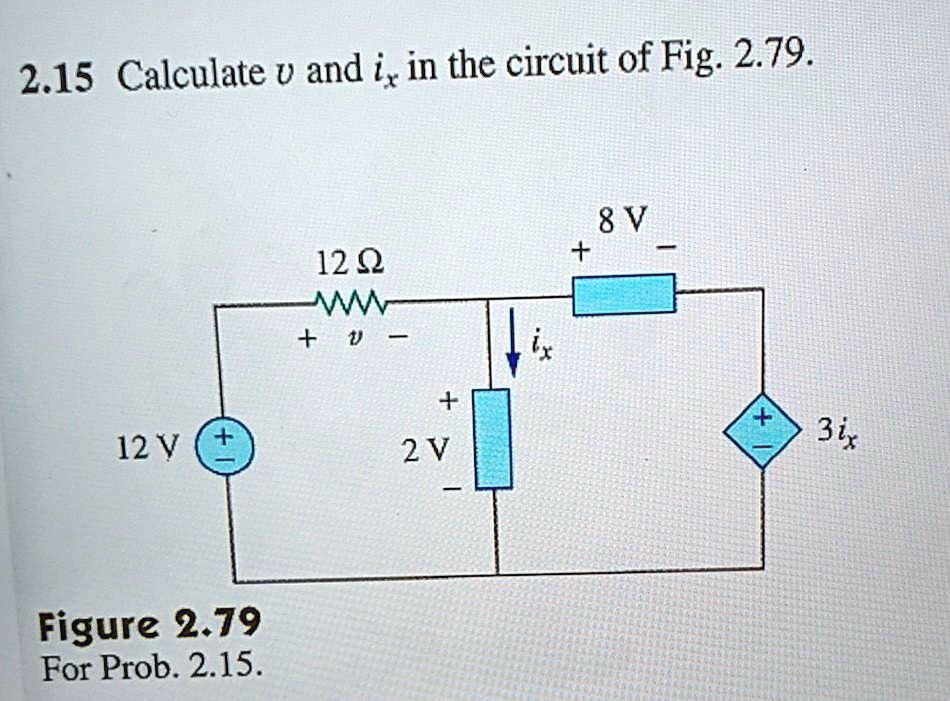
Calculate v and ix in the circuit of Fig. 2.79.
The Correct Answer and Explanation is:
v = 10 V — iₓ = 10/3 A
To determine the values of the voltage v and the current iₓ in the provided circuit, we can apply Kirchhoff’s Voltage Law (KVL), which states that the algebraic sum of all voltages around any closed loop in a circuit is equal to zero. This circuit can be analyzed by considering its two distinct loops: the left loop and the right loop.
1. Analysis of the Left Loop to find v:
The left loop consists of the 12 V independent voltage source, the 12 Ω resistor (with voltage v across it), and the 2 V independent voltage source. We can traverse this loop, starting from the bottom-left corner and moving clockwise.
- Moving up through the 12 V source, we go from the negative to the positive terminal, which is a voltage rise of +12 V.
- Moving across the 12 Ω resistor, we follow the direction of the indicated voltage drop v (from + to -), so we subtract v.
- Moving down through the 2 V source, we go from the positive to the negative terminal, which is a voltage drop of -2 V.
Setting up the KVL equation for the left loop:
+12 V – v – 2 V = 0
Now, we can solve for v:
10 V – v = 0
v = 10 V
2. Analysis of the Right Loop to find iₓ:
The right loop contains the 2 V independent voltage source, the 8 V independent voltage source, and the 3iₓ current-controlled dependent voltage source. We can traverse this loop, starting from the bottom of the 2 V source and moving clockwise.
- Moving up through the 2 V source, we go from negative to positive, which is a voltage rise of +2 V.
- Moving across the 8 V source, we go from negative to positive, which is a voltage rise of +8 V.
- Moving down through the dependent voltage source, we go from its positive to its negative terminal, which is a voltage drop of -3iₓ.
Setting up the KVL equation for the right loop:
+2 V + 8 V – 3iₓ = 0
Now, we can solve for iₓ:
10 V – 3iₓ = 0
3iₓ = 10 V
iₓ = 10/3 A (or approximately 3.33 A)
Therefore, by applying KVL to the two independent loops in the circuit, we find that the voltage v is 10 V and the current iₓ is 10/3 A.
