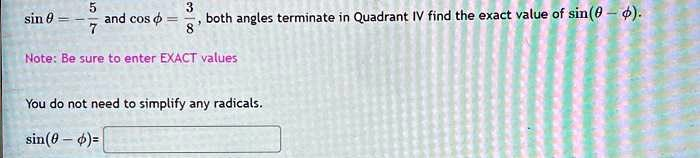
sinθ =and cosϕ=3 /8, both angles terminate in Quadrant IV find the exact value of sin(θ−ϕ).
The Correct Answer and Explanation is:
To find the exact value of sin(θ — φ), we will use the sine difference identity:
sin(θ — φ) = sin(θ)cos(φ) — cos(θ)sin(φ)
We are given the following information:
- sin(θ) = -5/7
- cos(φ) = 3/8
- Both angles θ and φ are in Quadrant IV.
We need to find the values of cos(θ) and sin(φ).
Step 1: Find cos(θ)
We use the Pythagorean identity sin²(θ) + cos²(θ) = 1.
(-5/7)² + cos²(θ) = 1
25/49 + cos²(θ) = 1
cos²(θ) = 1 – 25/49
cos²(θ) = 49/49 – 25/49
cos²(θ) = 24/49
cos(θ) = ±√(24/49) = ±√24 / 7
Since θ is in Quadrant IV, its cosine value is positive.
Therefore, cos(θ) = √24 / 7.
Step 2: Find sin(φ)
We use the Pythagorean identity again: sin²(φ) + cos²(φ) = 1.
sin²(φ) + (3/8)² = 1
sin²(φ) + 9/64 = 1
sin²(φ) = 1 – 9/64
sin²(φ) = 64/64 – 9/64
sin²(φ) = 55/64
sin(φ) = ±√(55/64) = ±√55 / 8
Since φ is in Quadrant IV, its sine value is negative.
Therefore, sin(φ) = -√55 / 8.
Step 3: Substitute the values into the sine difference formula
Now we have all the necessary components:
- sin(θ) = -5/7
- cos(φ) = 3/8
- cos(θ) = √24 / 7
- sin(φ) = -√55 / 8
Substitute these into the formula sin(θ — φ) = sin(θ)cos(φ) — cos(θ)sin(φ):
sin(θ — φ) = (-5/7)(3/8) — (√24 / 7)(-√55 / 8)
sin(θ — φ) = -15/56 — (-√(24 * 55) / 56)
sin(θ — φ) = -15/56 + √1320 / 56
sin(θ — φ) = (-15 + √1320) / 56
The problem states not to simplify radicals, so this is the final exact form.
sin(θ — φ) = (-15 + √1320)/56
