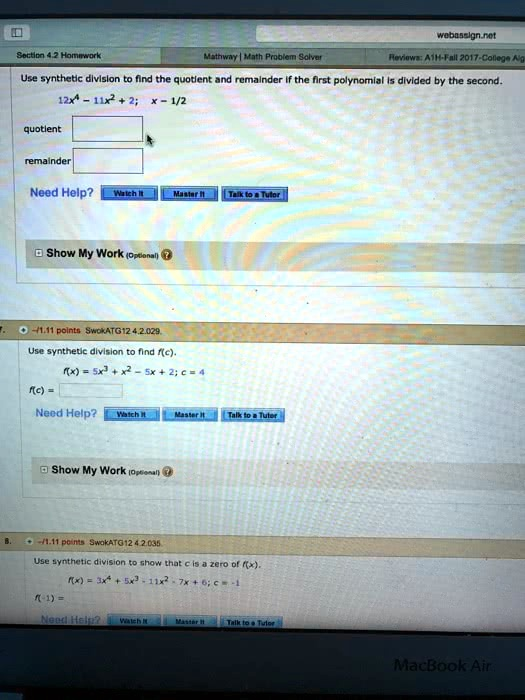
Use synthetic division to find the quotient and remainder if the first polynomial is divided by the second
The Correct Answer and Explanation is:
Of course. Here is the correct answer and a detailed explanation for the math problem.
quotient — 12x³ + 6x² – 8x – 4
remainder — 0
Explanation
The problem asks to use synthetic division to divide the polynomial 12x⁴ – 11x² + 2 by x – 1/2. Synthetic division is a simplified method of polynomial division, specifically used when the divisor is a linear expression of the form x – c.
Step 1: Set up the Division
First, identify the coefficients of the dividend polynomial, 12x⁴ – 11x² + 2. It’s crucial to list the coefficients for every power of x in descending order, from the highest power down to the constant term. If a term is missing, we must use a zero as a placeholder. In this case, the x³ and x terms are missing.
The polynomial can be rewritten as: 12x⁴ + 0x³ – 11x² + 0x + 2.
The coefficients are: 12, 0, -11, 0, 2.
Next, identify the value of c from the divisor, x – c. For the divisor x – 1/2, the value of c is 1/2.
We set up the synthetic division problem by writing c to the left and the coefficients of the dividend to the right:Generated code
1/2 | 12 0 -11 0 2
|
-----------------------Step 2: Perform the Synthetic Division
- Bring down the first coefficient (12) below the line.
- Multiply this number (12) by c (1/2): 12 * (1/2) = 6. Write this result under the second coefficient (0).
- Add the numbers in the second column: 0 + 6 = 6.
- Repeat the process: multiply the new number (6) by c: 6 * (1/2) = 3. Write this under the third coefficient (-11) and add: -11 + 3 = -8.
- Continue this pattern: -8 * (1/2) = -4. Write this under the next coefficient (0) and add: 0 + (-4) = -4.
- For the final step: -4 * (1/2) = -2. Write this under the last coefficient (2) and add: 2 + (-2) = 0.
The completed division looks like this:Generated code
1/2 | 12 0 -11 0 2
| 6 3 -4 -2
--------------------------
12 6 -8 -4 0Step 3: Interpret the Result
The numbers in the bottom row represent the coefficients of the quotient and the remainder. The last number, 0, is the remainder. The other numbers, 12, 6, -8, -4, are the coefficients of the quotient polynomial.
The degree of the quotient is always one less than the degree of the dividend. Since the dividend was a 4th-degree polynomial, the quotient will be a 3rd-degree polynomial. Using the coefficients from our result, the quotient is 12x³ + 6x² – 8x – 4.
