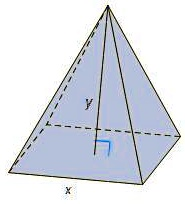
A square pyramid has a base with side length x and a height y. Find the volume of the pyramid.
The Correct Answer and Explanation is:
The volume VVV of a pyramid can be found using the formula:V=13×Base Area×HeightV = \frac{1}{3} \times \text{Base Area} \times \text{Height}V=31×Base Area×Height
For a square pyramid, the base area is simply the area of a square, which is given by:Base Area=x2\text{Base Area} = x^2Base Area=x2
where xxx is the length of a side of the square base. The height yyy is the perpendicular distance from the apex to the center of the square base.
Thus, the volume of the pyramid is:V=13×x2×yV = \frac{1}{3} \times x^2 \times yV=31×x2×y
Explanation:
- Base Area: The base of the pyramid is a square, so its area is x2x^2×2.
- Height: The height of the pyramid is the perpendicular distance from the apex to the center of the base, denoted by yyy.
- Volume Formula: The formula for the volume of a pyramid is always 13×Base Area×Height\frac{1}{3} \times \text{Base Area} \times \text{Height}31×Base Area×Height, which accounts for the shape’s tapering from the base to the apex.
Therefore, the volume of the pyramid is 13x2y\frac{1}{3} x^2 y31x2y.
