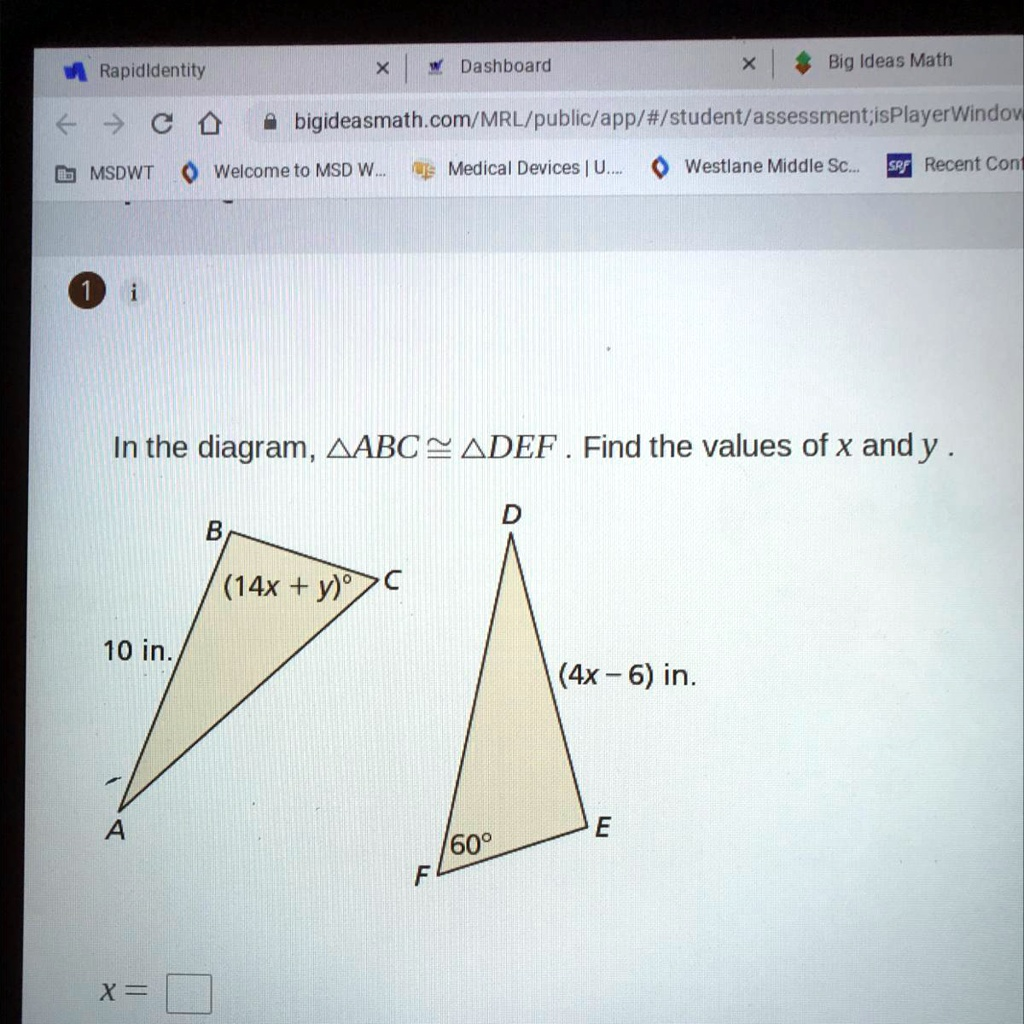
Find the values of x and y
The Correct Answer and Explanation is:
Based on the provided image, here are the values for x and y.
Correct Answer:
x = 4
y = 4
Explanation:
The problem states that triangle ABC is congruent to triangle DEF, written as ΔABC ≅ ΔDEF. This congruence means that all corresponding parts of the two triangles—their sides and angles—are equal. The order of the vertices in the congruence statement tells us which parts correspond.
- Corresponding Sides:
- Side AB corresponds to side DE.
- Side BC corresponds to side EF.
- Side AC corresponds to side DF.
- Corresponding Angles:
- Angle A corresponds to Angle D (∠A ≅ ∠D).
- Angle B corresponds to Angle E (∠B ≅ ∠E).
- Angle C corresponds to Angle F (∠C ≅ ∠F).
Step 1: Find the value of x.
From the diagram, we are given the lengths of the corresponding sides AB and DE.
- Length of AB = 10 in.
- Length of DE = (4x – 6) in.
Since AB and DE are corresponding sides of congruent triangles, their lengths must be equal. We can set up an equation:
AB = DE
10 = 4x – 6
To solve for x, first add 6 to both sides of the equation:
10 + 6 = 4x
16 = 4x
Now, divide both sides by 4:
x = 16 / 4
x = 4
Step 2: Find the value of y.
From the diagram, we are given the measures of the corresponding angles C and F.
- Measure of Angle C = (14x + y)°
- Measure of Angle F = 60°
Since ∠C and ∠F are corresponding angles, their measures are equal. We can set up another equation:
m∠C = m∠F
14x + y = 60
We already found that x = 4. We can substitute this value into the equation to solve for y:
14(4) + y = 60
56 + y = 60
To find y, subtract 56 from both sides of the equation:
y = 60 – 56
y = 4
Thus, the values are x = 4 and y = 4.
