Carbonic acid (H2CO3) is a diprotic acid with Ka1=4.3×10−7; Ka2=5.6×10−11.

) Carbonic acid (H2CO3) is a diprotic acid with Ka1=4.3×10−7; Ka2=5.6×10−11.

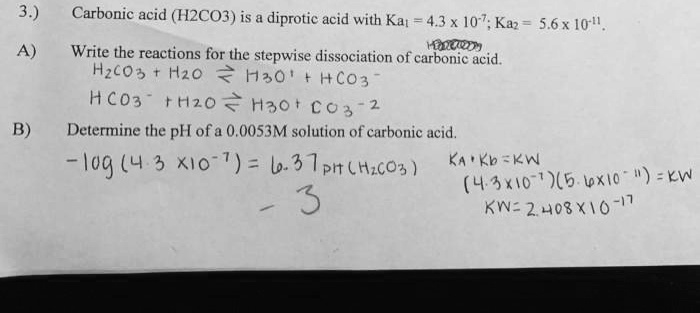
The Correct Answer and Explanation is:

Here is the correct solution to the problem presented in the image.

A) Write the reactions for the stepwise dissociation of carbonic acid.
The handwritten reactions are correct. Carbonic acid (H₂CO₃) is a diprotic acid, meaning it can donate two protons in a stepwise manner.

• First dissociation:
  H₂CO₃(aq) + H₂O(l) ⇌ H₃O⁺(aq) + HCO₃⁻(aq)
  This step is associated with the first acid dissociation constant, Ka₁ = 4.3 x 10⁻⁷.
• Second dissociation:
  HCO₃⁻(aq) + H₂O(l) ⇌ H₃O⁺(aq) + CO₃²⁻(aq)
  This step is associated with the second acid dissociation constant, Ka₂ = 5.6 x 10⁻¹¹.

B) Determine the pH of a 0.0053 M solution of carbonic acid.
The correct pH is 4.32.

The handwritten calculation is incorrect. The calculation -log(4.3 x 10⁻⁷) = 6.37 determines the pKa₁ of carbonic acid, not the pH of the solution. The pH depends on both the acid’s strength (Ka) and its initial concentration.

Here is the correct method to determine the pH:

1. Analyze the Dissociation Steps: To find the pH, we need the concentration of hydronium ions, [H₃O⁺], at equilibrium. Since carbonic acid is diprotic, both dissociation reactions produce H₃O⁺. However, because Ka₁ (4.3 x 10⁻⁷) is much larger than Ka₂ (5.6 x 10⁻¹¹), the first dissociation is the dominant source of H₃O⁺ ions. The contribution from the second dissociation is negligible and can be ignored for the initial pH calculation.
2. Use an ICE Table for the First Dissociation: We set up an ICE (Initial, Change, Equilibrium) table for the first dissociation to find the equilibrium concentrations. Let ‘x’ be the change in concentration.ReactionH₂CO₃H₃O⁺HCO₃⁻Initial (I)0.0053 M~0 M0 MChange (C)-x+x+xEquilibrium (E)0.0053 – xxx
3. Use the Ka₁ Expression: Now, we write the expression for Ka₁ and substitute the equilibrium values.Ka₁ = [H₃O⁺][HCO₃⁻] / [H₂CO₃]
   4.3 x 10⁻⁷ = (x)(x) / (0.0053 – x)
4. Simplify and Solve for x: Because Ka₁ is very small compared to the initial concentration, we can assume that ‘x’ is negligible compared to 0.0053 M (i.e., 0.0053 – x ≈ 0.0053). This assumption is valid if the initial concentration divided by Ka₁ is greater than 100. Here, 0.0053 / (4.3 x 10⁻⁷) is approximately 12,325, so the approximation is justified.4.3 x 10⁻⁷ ≈ x² / 0.0053
   x² = (4.3 x 10⁻⁷) * (0.0053)
   x² = 2.279 x 10⁻⁹
   x = √(2.279 x 10⁻⁹)
   x ≈ 4.77 x 10⁻⁵ M
5. Calculate the pH: The value of x represents the equilibrium concentration of H₃O⁺.[H₃O⁺] = 4.77 x 10⁻⁵ M
   pH = -log[H₃O⁺]
   pH = -log(4.77 x 10⁻⁵)
   pH ≈ 4.32