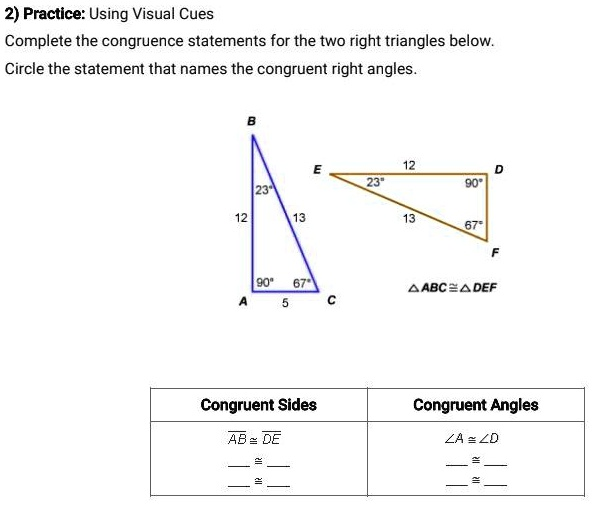
Using Visual Cues Complete the congruence statements for the two right triangles below.

Using Visual Cues Complete the congruence statements for the two right triangles below.

The Correct Answer and Explanation is:

Of course. Here is the completed solution and a detailed explanation.

Completed Congruence Statements

Congruent SidesGenerated code

AB ≅ DE
BC ≅ EF
AC ≅ DF

Congruent Angles

∠A ≅ ∠D   <-- This statement names the congruent right angles.
∠B ≅ ∠E
∠C ≅ ∠F

Explanation

The problem requires us to identify the corresponding congruent sides and angles of the two right triangles, ABC and DEF, based on the provided visual cues and the given congruence statement, ΔABC ≅ ΔDEF.

The statement ΔABC ≅ ΔDEF is the most important piece of information. It tells us that the two triangles are congruent and also specifies which vertices correspond to each other. The order of the letters is critical:

• A corresponds to D.
• B corresponds to E.
• C corresponds to F.

Using this correspondence, we can determine all the pairs of congruent parts. This principle is often referred to as “Corresponding Parts of Congruent Triangles are Congruent” (CPCTC).

Finding Congruent Sides:
We match the vertices in pairs to find the congruent sides:

1. Side AB (first and second letters of ΔABC) corresponds to side DE (first and second letters of ΔDEF). The diagram confirms this, showing both sides have a length of 12.
2. Side BC (second and third letters) corresponds to side EF (second and third letters). The diagram confirms this, as both are hypotenuses with a length of 13.
3. Side AC (first and third letters) corresponds to side DF (first and third letters). The diagram shows side AC has a length of 5, so side DF must also have a length of 5.

Finding Congruent Angles:
We match the individual vertices to find the congruent angles:

1. Angle A (first letter) corresponds to Angle D (first letter). The diagram shows both are right angles, measuring 90°.
2. Angle B (second letter) corresponds to Angle E (second letter). The diagram confirms this, showing both angles measure 23°.
3. Angle C (third letter) corresponds to Angle F (third letter). The diagram confirms this, showing both angles measure 67°.

The final instruction is to identify the statement that names the congruent right angles. Since Angle A and Angle D both measure 90°, they are the right angles. Therefore, the correct statement is ∠A ≅ ∠D.