The Correct Answer and Explanation is:
Based on the information provided, a logical derived value is the base dissociation constant (Kₑ) for the conjugate base of nitrous acid.
Correct Answer: The base dissociation constant (Kₑ) for the nitrite ion (NO₂⁻) at 25 °C is 2.2 × 10⁻¹¹.
Explanation
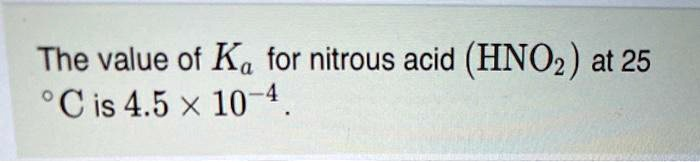
The information provided states that the acid dissociation constant (Kₐ) for nitrous acid (HNO₂) is 4.5 × 10⁻⁴ at 25 °C. This value is a quantitative measure of the strength of nitrous acid in a solution. The Kₐ corresponds to the equilibrium constant for the dissociation of the acid in water, as shown in the reaction:
HNO₂(aq) + H₂O(l) ⇌ H₃O⁺(aq) + NO₂⁻(aq)
The Kₐ expression is [H₃O⁺][NO₂⁻] / [HNO₂]. Since the Kₐ value of 4.5 × 10⁻⁴ is significantly less than 1, it confirms that nitrous acid is a weak acid. This means that at equilibrium, the majority of the acid remains in its undissociated molecular form (HNO₂) rather than splitting into hydronium ions (H₃O⁺) and nitrite ions (NO₂⁻).
From the Kₐ of a weak acid, we can determine the strength of its conjugate base. For nitrous acid (HNO₂), the conjugate base is the nitrite ion (NO₂⁻). The strength of this conjugate base is described by its base dissociation constant, Kₑ.
At a given temperature, the product of the Kₐ for an acid and the Kₑ for its conjugate base is equal to the ion-product constant for water, Kₙ. At 25 °C, Kₙ is a constant with the value 1.0 × 10⁻¹⁴. The relationship is expressed as:
Kₐ × Kₑ = Kₙ
Using this equation, we can calculate the Kₑ for the nitrite ion:
Kₑ = Kₙ / Kₐ
Kₑ = (1.0 × 10⁻¹⁴) / (4.5 × 10⁻⁴)
Kₑ = 2.2 × 10⁻¹¹
This calculated Kₑ value of 2.2 × 10⁻¹¹ indicates that the nitrite ion is a very weak base, which is expected for the conjugate base of a weak acid. This fundamental relationship allows chemists to understand and predict the behavior of both acidic and basic species in a solution.
