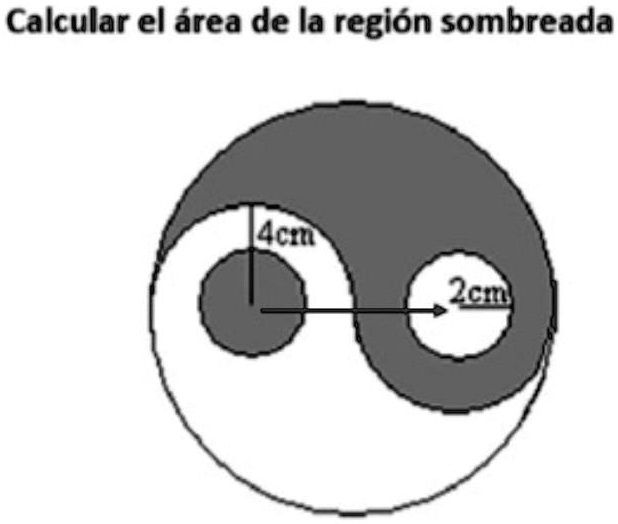
Calcular el área de la región sombreada ayudaa porfa con explicación Calcular el área de la región sombreada Acm 2cm
The Correct Answer and Explanation is:
Of course! Here is the calculation and a detailed explanation for finding the area of the shaded region.
Correct Answer: The area of the shaded region is 8π cm².
Explanation
To find the area of the shaded region, we can use a simple and elegant method based on symmetry and rearranging the shapes. This avoids complex calculations by recognizing how the different parts of the figure relate to each other.
1. Identify the Components
The total shaded area is composed of three distinct parts:
- The large, dark, S-shaped swirl.
- A small, white circular area that has been removed from the swirl.
- A small, dark circular area that has been added in the white half of the symbol.
The problem can be written as an equation:
Shaded Area = (Area of the dark swirl) – (Area of the small white circle) + (Area of the small dark circle)
2. Use the Principle of Symmetry
The image is a variation of the classic Yin-Yang symbol, which is built on symmetry. We can see that the small white circle removed from the dark area is identical in size to the small dark circle added to the white area. Because their sizes are identical, their areas are equal.
- Area of the small white circle = Area of the small dark circle
When we look at our equation, the two small circles cancel each other out. The area we subtract for the white hole is immediately added back by the dark circle. Therefore, the problem simplifies significantly:
Shaded Area = Area of the dark swirl
3. Calculate the Area of the Swirl
The S-shaped curve perfectly divides the large, main circle into two equal regions: the dark swirl and the white swirl. This means the area of the dark swirl is exactly half the area of the entire large circle.
4. Determine the Radius and Calculate the Final Area
The diagram provides the necessary dimension to find the area of the large circle. The vertical line labeled “4cm” indicates the radius of the large circle, extending from its center to the top edge.
- Radius of the large circle (R) = 4 cm
Now, we can calculate the area of the full circle using the formula A = πR²:
- Area of large circle = π * (4 cm)² = 16π cm²
Since the shaded area is half of the total area, we get:
- Area of shaded region = (1/2) * (Area of large circle) = (1/2) * 16π cm² = 8π cm²
