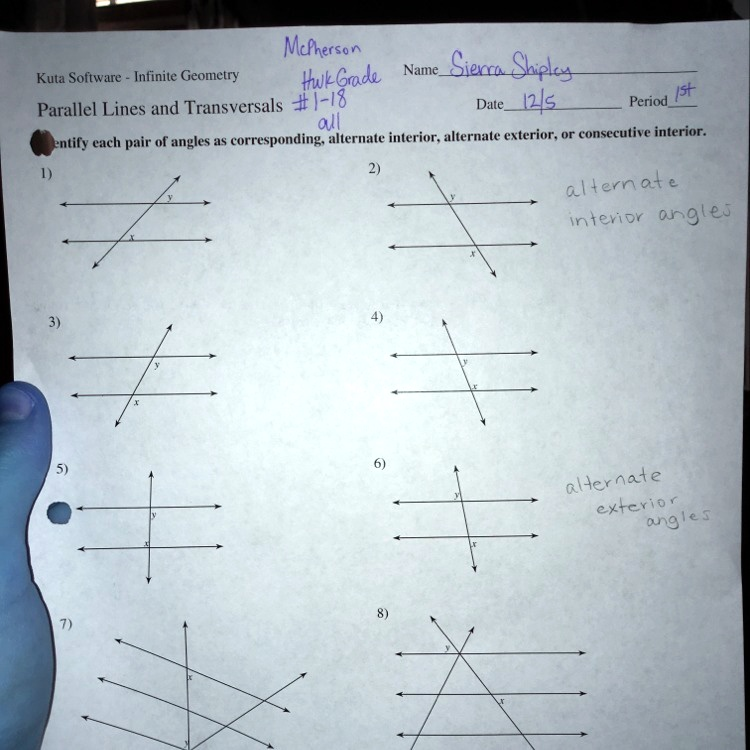
McPherson Kuta Software – Infinite Geometry Hwk Grade Name Sierra Shipley Date 12/5 Period 1st Parallel Lines and Transversals #1-18 all entify each pair of angles as corresponding, alternate interior, alternate exterior, or consecutive interior. 1) 3) 5) 7) y y 2) 4) 6) 8) X ? alternate interior angles alternate exterior angles
The Correct Answer and Explanation is:
Based on the geometry worksheet provided, the correct answer for the unlabeled problem #1 is consecutive interior angles.
Explanation
In the field of geometry, understanding the relationships between angles formed by parallel lines and a transversal is a fundamental concept. A transversal is a line that intersects two or more other lines, which in this worksheet are presented as parallel. The intersection of the transversal with the two parallel lines creates eight distinct angles, and these angles have special relationships with one another.
To correctly identify the relationship between angles x and y in the first problem, we must first define the different regions created by this intersection. The space located between the two parallel lines is known as the interior region. Conversely, the space located outside of the two parallel lines is the exterior region.
With these regions defined, we can classify the pairs of angles. The worksheet asks to identify one of four specific relationships: corresponding, alternate interior, alternate exterior, or consecutive interior angles.
- Alternate interior angles are found on opposite sides of the transversal but within the interior region.
- Alternate exterior angles are similarly on opposite sides of the transversal, but they lie in the exterior region.
- Corresponding angles occupy the same relative position at each of the two intersections. For example, the top left angle at one intersection corresponds to the top left angle at the other.
This brings us to the final type, consecutive interior angles, which are also known as same side interior angles. This classification applies to a pair of angles that are both located in the interior region, between the parallel lines, and are also on the same side of the transversal.
Looking closely at problem 1, we can see that angle x is located at the lower intersection, and it is positioned between the two parallel lines. It is also on the left side of the slanting transversal. Similarly, angle y is at the upper intersection, also positioned between the two parallel lines and on the left side of the transversal. Because both angles are in the interior region and on the same side of the transversal, their relationship is defined as consecutive interior angles. A key property of these angles, when the lines are parallel, is that they are supplementary, meaning their measures add up to 180 degrees.
