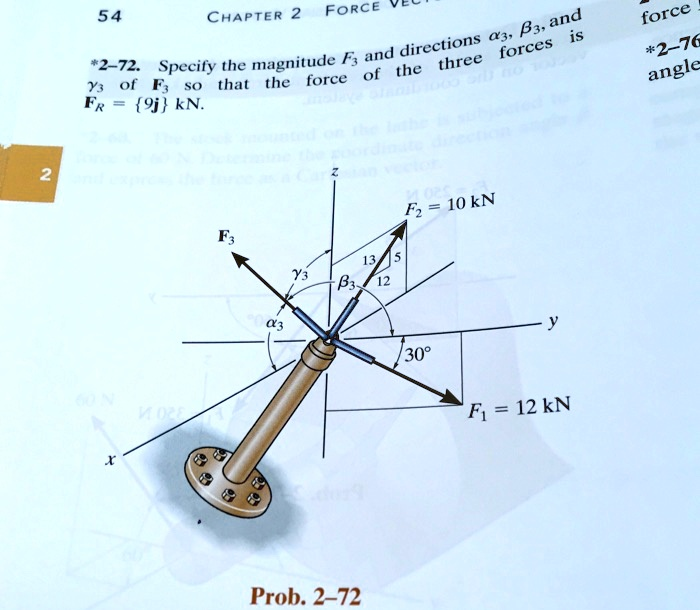
Specify the magnitude F3 and directions α₃ , ,β₃ and of so that the force of the three forces is
The Correct Answer and Explanation is:
Correct Answer:
The magnitude and direction angles of the force F₃ are:
- F₃ = 10.6 kN
- α₃ = 125°
- β₃ = 42.3°
- γ₃ = 111°
Explanation:
To determine the properties of force F₃, we use the principle of vector addition. The resultant force, F_R, is the vector sum of the three individual forces: F_R = F₁ + F₂ + F₃. The problem requires this resultant to be F_R = {9j} kN.
First, we must express each force in its Cartesian vector components (i, j, k).
Force F₁ has a magnitude of 12 kN and lies in the x-y plane. Its components are found using trigonometry, with the angle 30° given with respect to the y-axis.
- F₁ₓ = 12 sin(30°) = 6 kN
- F₁ᵧ = 12 cos(30°) = 10.39 kN
- F₁ = {6i + 10.39j} kN
Force F₂ has a magnitude of 10 kN and lies in the y-z plane. Its components are determined using the provided 5-12-13 slope triangle. It acts in the negative y and positive z directions.
- F₂ᵧ = -10 * (12/13) = -9.23 kN
- F₂z = 10 * (5/13) = 3.85 kN
- F₂ = {-9.23j + 3.85k} kN
The unknown force is F₃ = {F₃ₓ i + F₃ᵧ j + F₃z k}.
Since the sum of the forces equals the resultant, we can equate the sum of the components on each axis:
- x-axis: 0 = F₁ₓ + F₂ₓ + F₃ₓ → 0 = 6 + 0 + F₃ₓ → F₃ₓ = -6 kN
- y-axis: 9 = F₁ᵧ + F₂ᵧ + F₃ᵧ → 9 = 10.39 – 9.23 + F₃ᵧ → F₃ᵧ = 7.84 kN
- z-axis: 0 = F₁z + F₂z + F₃z → 0 = 0 + 3.85 + F₃z → F₃z = -3.85 kN
With the components of F₃ known, we find its magnitude using the 3D Pythagorean theorem:
F₃ = √(F₃ₓ² + F₃ᵧ² + F₃z²) = √((-6)² + (7.84)² + (-3.85)²) ≈ 10.6 kN.
The direction angles are then found using the inverse cosine of each component divided by the magnitude:
- α₃ = arccos(F₃ₓ / F₃) = arccos(-6 / 10.6) ≈ 125°
- β₃ = arccos(F₃ᵧ / F₃) = arccos(7.84 / 10.6) ≈ 42.3°
- γ₃ = arccos(F₃z / F₃) = arccos(-3.85 / 10.6) ≈ 111°
