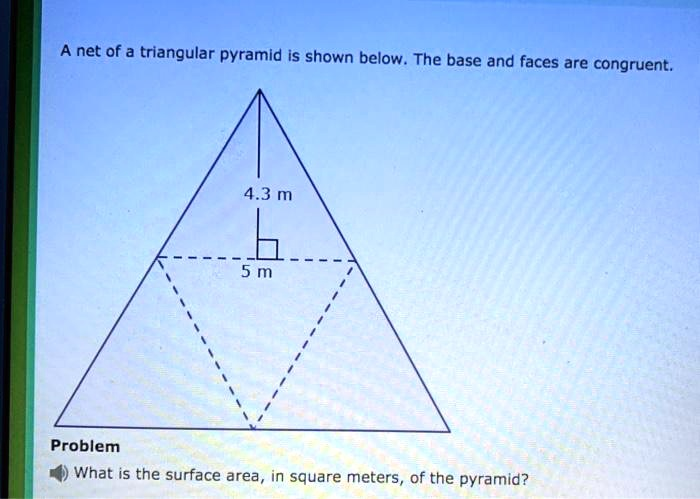
A net of a triangular pyramid is shown below. The base and faces are congruent: 4.3 m 5 m Problem What is the surface area in square meters, of the pyramid?
The Correct Answer and Explanation is:
The correct answer is 43 square meters.
To find the surface area of the pyramid, we need to calculate the total area of all its faces. The image displays the pyramid’s net, which is the shape made by unfolding the three dimensional pyramid into a flat, two dimensional figure. The total area of this net is the surface area of the pyramid.
The problem states that the base and the faces of the pyramid are congruent. A triangular pyramid has one triangular base and three triangular side faces, for a total of four surfaces. The fact that they are all congruent means the net is composed of four identical triangles.
The diagram provides the dimensions for one of these triangles. We can calculate its area using the standard formula for the area of a triangle:
Area = (1/2) × base × height
According to the diagram, the dimensions are:
Base (b) = 5 meters
Height (h) = 4.3 meters
Plugging these values into the formula gives us the area of a single triangle:
Area of one triangle = (1/2) × 5 m × 4.3 m
Area of one triangle = 2.5 m × 4.3 m
Area of one triangle = 10.75 square meters
Since the pyramid is made of four of these identical triangles, we find the total surface area by multiplying the area of one triangle by four.
Total Surface Area = Area of one triangle × 4
Total Surface Area = 10.75 m² × 4
Total Surface Area = 43 m²
Thus, the surface area of the pyramid is 43 square meters.
