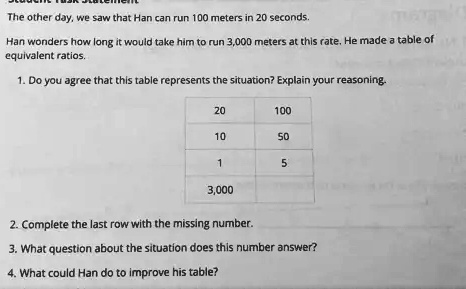
The other day, we saw that Han can run 100 meters in 20 seconds. Han wonders how long it would take him to run 3,000 meters at this rate. He made a table of equivalent ratios. 1. Do you agree that this table represents the situation? Explain your reasoning. 20 100 10 50 1 5 3,000 2. Complete the last row with the missing number. 3. What question about the situation does this number answer? 4. What could Han do to improve his table?
The Correct Answer and Explanation is:
Here are the answers to the questions based on the image provided.
1. Do you agree that this table represents the situation? Explain your reasoning.
No, the table does not correctly represent the situation Han is trying to solve. The first three rows of the table correctly show equivalent ratios based on the initial information. The first row shows 100 meters run in 20 seconds. The next rows correctly calculate that this is equivalent to running 50 meters in 10 seconds, and a unit rate of 5 meters in 1 second.
The error is in the last row. Han wants to find the time it takes to run 3,000 meters. In his table, the right column represents distance in meters, and the left column represents time in seconds. Han incorrectly placed the distance value, 3,000, in the time column. Therefore, the setup in the final row does not align with the question he wants to answer.
2. Complete the last row with the missing number.
Following the pattern in the table as Han incorrectly created it, the missing number is 15,000.
To maintain an equivalent ratio based on the third row (1 to 5), if the number in the first column is 3,000, you must multiply the number in the second column by the same factor. To get from 1 to 3,000, you multiply by 3,000. Applying this to the second column: 5 * 3,000 = 15,000.
3. What question about the situation does this number answer?
The number 15,000 answers the question: “How many meters would Han run in 3,000 seconds?”
The completed row [3,000, 15,000] signifies that at his established rate, 3,000 seconds of running would cover a distance of 15,000 meters. This is different from Han’s original question, which was how long it would take to run 3,000 meters. The correct answer to his original question is 600 seconds, found by dividing the target distance by his speed (3,000 meters / 5 meters per second).
4. What could Han do to improve his table?
Han could make two key improvements to his table. First, he should add labels or headings to the columns, such as “Time (seconds)” and “Distance (meters)”. This would make the table’s structure clear and help prevent mistakes.
Second, to answer his original question correctly, he should have placed the number 3,000 in the distance column (the right column) and then calculated the missing value in the time column (the left column). This would have led him to the correct answer of 600 seconds.
