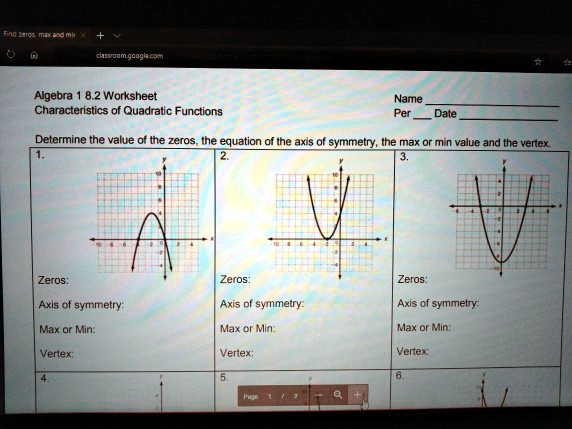
Find zeros, max and min classroom.google.com Algebra 1 8.2 Worksheet Characteristics of Quadratic Functions Name Per____Date____ Determine the value of the zeros, the equation of the axis of symmetry, the max or min value and the vertex. 1. 2. 3. Zeros: Axis of symmetry: Max or Min: Vertex: 4 Zeros: Axis of symmetry: Max or Min: Vertex: 5. Zeros: Axis of symmetry: Max or Min: Vertex: 6. Page 1/2 Q
The Correct Answer and Explanation is:
Let’s analyze each of the three graphs (problems 1 to 3) from the worksheet titled “Characteristics of Quadratic Functions”. For each graph, we will identify the zeros, axis of symmetry, maximum or minimum, and vertex based on the visual data.
Problem 1:
- Zeros: The parabola crosses the x-axis at x = -3 and x = 1.
- Axis of Symmetry: The vertical line halfway between the zeros is at x = -1.
- Max or Min: The parabola opens downward, so it has a maximum.
- Vertex: The vertex is the highest point, located at (-1, 4).
Problem 2:
- Zeros: The graph does not cross the x-axis, so there are no real zeros.
- Axis of Symmetry: The parabola is symmetric about the line x = 0.
- Max or Min: The parabola opens upward, so it has a minimum.
- Vertex: The vertex is at (0, -3).
Problem 3:
- Zeros: The parabola crosses the x-axis at x = -4 and x = 2.
- Axis of Symmetry: The midpoint of the zeros is at x = -1.
- Max or Min: It opens upward, so it has a minimum.
- Vertex: The vertex lies at (-1, -4).
Explanation
Quadratic functions are represented by parabolas on a graph. The zeros of a quadratic function are the x-values where the graph intersects the x-axis, also known as the roots or solutions of the equation. These points occur when the output (y) value is zero.
The axis of symmetry is a vertical line that divides the parabola into two mirror-image halves. It always passes through the vertex, which is the highest or lowest point of the graph depending on the direction the parabola opens. You can find the axis of symmetry by averaging the x-values of the two zeros when they exist, using the formula x=x1+x22x = \frac{x_1 + x_2}{2}x=2×1+x2.
The vertex is the turning point of the parabola. If the parabola opens upwards (like a U), the vertex is the minimum point. If it opens downwards (like an upside-down U), the vertex is the maximum point. This tells us whether the function has a maximum or minimum value.
In this worksheet, problem 1’s graph has a maximum since it opens down, while problems 2 and 3 have minimums because they open up. Identifying these characteristics helps understand the shape and behavior of quadratic functions, which is useful in solving real-world problems involving area, trajectory, and optimization.
