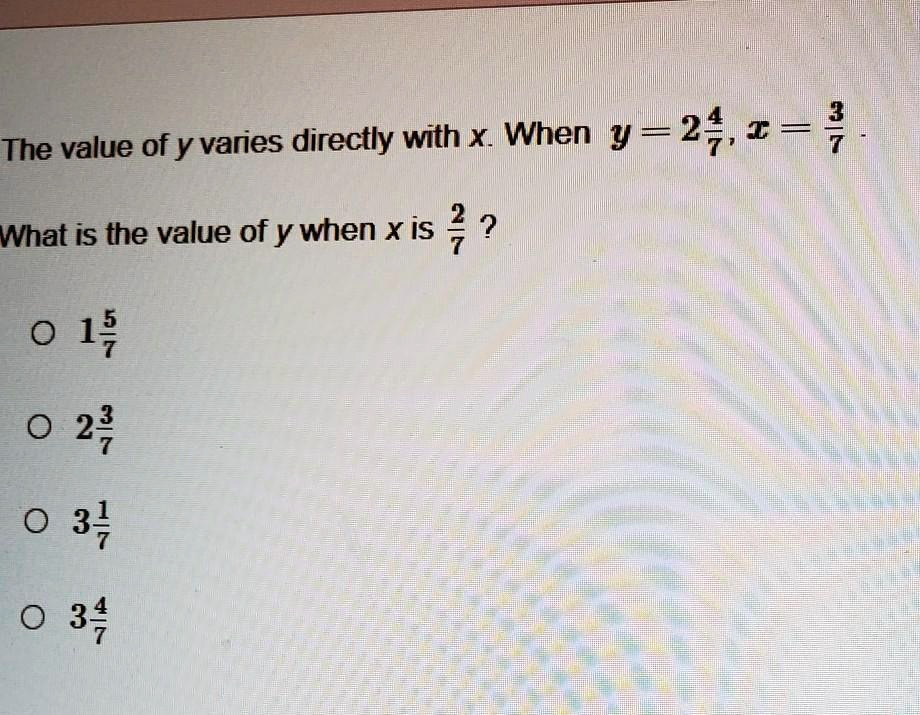
The Correct Answer and Explanation is:
Correct Answer: 1 5/7
📘 Explanation
This problem involves the concept of direct variation, which describes a relationship between two variables where one is a constant multiple of the other. Mathematically, this is expressed as:
y=kxy = kx
Here, yy varies directly with xx, meaning the ratio yx\frac{y}{x} remains constant. This constant is denoted by kk, the constant of variation.
We are given:
- y=247y = 2 \frac{4}{7}
- x=37x = \frac{3}{7}
First, convert the mixed number y=247y = 2 \frac{4}{7} into an improper fraction:
247=1872 \frac{4}{7} = \frac{18}{7}
Now, calculate the constant of variation kk:
k=yx=187÷37=187×73=12621=6k = \frac{y}{x} = \frac{18}{7} \div \frac{3}{7} = \frac{18}{7} \times \frac{7}{3} = \frac{126}{21} = 6
So, k=6k = 6. This means for any value of xx, the corresponding value of yy is 6x6x.
Now, we are asked to find the value of yy when x=27x = \frac{2}{7}:
y=6×27=127y = 6 \times \frac{2}{7} = \frac{12}{7}
Convert 127\frac{12}{7} into a mixed number:
127=157\frac{12}{7} = 1 \frac{5}{7}
Thus, the value of yy when x=27x = \frac{2}{7} is 1 5/7.
This solution demonstrates how direct variation allows us to maintain a consistent relationship between variables. By finding the constant of variation, we can easily compute new values without needing a graph or table.
