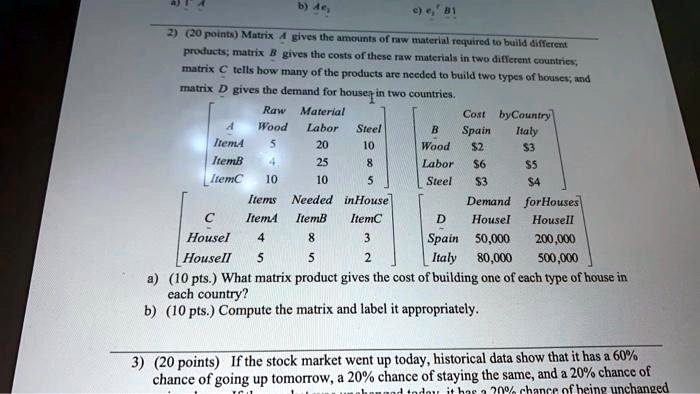
Matrix A gives the amounts of raw material required to build different products; matrix B gives the costs of these raw materials in two different countries, matrix C tells how many of the products are needed to build two types of houses; and matrix D gives the demand for house in two countries.
The Correct Answer and Explanation is:
Correct Answer
a) The matrix product that gives the cost of building one of each type of house in each country is C * A * B.
b) The computed and labeled matrix is:
| Spain | Italy | |
| House I | $2,381 | $2,272 |
| House II | $1,900 | $1,820 |
Which can be written as the matrix
[ 2381 2272 ]
[ 1900 1820 ]Explanation
This problem requires a chain of matrix multiplications to connect the initial components to the final desired outcome, which is the cost per house type in each country. We can solve this by thinking about the units we need to combine and cancel.
Our goal is a matrix where the rows represent the house types (House I, House II) and the columns represent the countries (Spain, Italy).
Step 1: Determine the total raw materials for each house type.
First, we need to find out the total amount of wood, labor, and steel required for each type of house. Matrix C tells us how many of each item (ItemA, ItemB, ItemC) are needed for each house. Matrix A tells us the raw materials (Wood, Labor, Steel) needed for each item. By multiplying Matrix C by Matrix A, we can find the total raw materials needed for each house type.
- Matrix C (2×3): [House Types] x [Items]
- Matrix A (3×3): [Items] x [Raw Materials]
The product C * A results in a 2×3 matrix representing [House Types] x [Raw Materials].
C * A = [ [4, 8, 3], [5, 5, 2] ] * [ [5, 20, 10], [4, 25, 8], [10, 10, 5] ]
C * A = [ [(20+32+30), (80+200+30), (40+64+15)], [(25+20+20), (100+125+20), (50+40+10)] ]
C * A = [ [82, 310, 119], [65, 245, 100] ]
This intermediate matrix tells us, for example, that House I requires 82 units of wood, 310 units of labor, and 119 units of steel.
Step 2: Calculate the cost in each country.
Now we have the raw materials per house. Matrix B gives the cost of each raw material in each country. We multiply our new matrix (C * A) by Matrix B to get the final cost.
- Matrix (C * A) (2×3): [House Types] x [Raw Materials]
- Matrix B (3×2): [Raw Materials] x [Country]
The product (C * A) * B will be a 2×2 matrix representing [House Types] x [Country], which is our desired result.
(C * A) * B = [ [82, 310, 119], [65, 245, 100] ] * [ [2, 3], [6, 5], [3, 4] ]
(C * A) * B = [ [(82*2 + 310*6 + 119*3)], [(82*3 + 310*5 + 119*4)] ]
[ [(65*2 + 245*6 + 100*3)], [(65*3 + 245*5 + 100*4)] ]
(C * A) * B = [ [(164 + 1860 + 357)], [(246 + 1550 + 476)] ]
[ [(130 + 1470 + 300)], [(195 + 1225 + 400)] ]
(C * A) * B = [ [2381, 2272], [1900, 1820] ]
This final matrix is labeled with House I and House II as rows and Spain and Italy as columns, providing the cost to build one of each house in each country.
