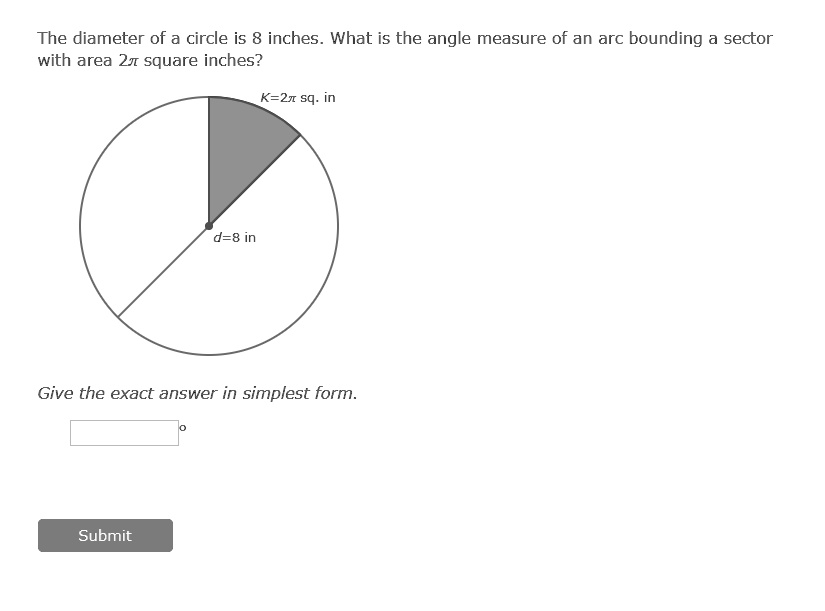
The diameter of a circle is 8 inches. What is the angle measure of an arc bounding a sector with an area of 2r square inches? K = θr sq. in d = 8 in Give the exact answer in simplest form. Submit
The Correct Answer and Explanation is:
To solve this problem, we will use the formula for the area of a sector of a circle, which is:A=θ360∘×πr2A = \frac{\theta}{360^\circ} \times \pi r^2A=360∘θ×πr2
Where:
- AAA is the area of the sector,
- θ\thetaθ is the central angle of the sector (in degrees),
- rrr is the radius of the circle.
Given:
- The diameter of the circle is 8 inches, so the radius r=82=4r = \frac{8}{2} = 4r=28=4 inches.
- The area of the sector is given as 2r2r2r, which is 2×4=82 \times 4 = 82×4=8 square inches.
We are asked to find the angle θ\thetaθ corresponding to this area. So, substituting into the sector area formula:8=θ360∘×π(4)28 = \frac{\theta}{360^\circ} \times \pi (4)^28=360∘θ×π(4)2
Simplifying the equation:8=θ360∘×π×168 = \frac{\theta}{360^\circ} \times \pi \times 168=360∘θ×π×168=16πθ360∘8 = \frac{16\pi\theta}{360^\circ}8=360∘16πθ8×360∘=16πθ8 \times 360^\circ = 16\pi\theta8×360∘=16πθ2880∘=16πθ2880^\circ = 16\pi\theta2880∘=16πθ
Now, solving for θ\thetaθ:θ=2880∘16π\theta = \frac{2880^\circ}{16\pi}θ=16π2880∘
Simplify:θ=180π degrees\theta = \frac{180}{\pi} \, \text{degrees}θ=π180degrees
So, the angle θ\thetaθ is 180π\frac{180}{\pi}π180 degrees.
This is the exact answer in its simplest form. To express it as a decimal, 180π≈57.3∘\frac{180}{\pi} \approx 57.3^\circπ180≈57.3∘, but the exact value is preferred when possible.
