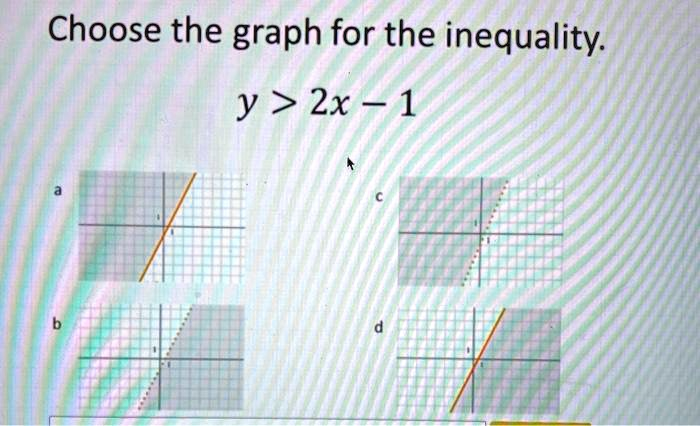
Choose the graph for the inequality: y > 2x – 1
The Correct Answer and Explanation is:
The correct answer is c.
To determine the correct graph for the inequality y > 2x – 1, we need to analyze two key components: the boundary line and the shaded region.
First, let’s consider the boundary line, which is represented by the equation y = 2x – 1. This equation is in the slope-intercept form y = mx + b, where m is the slope and b is the y-intercept.
- The y-intercept (b) is -1. This means the line must cross the vertical y-axis at the point (0, -1).
- The slope (m) is 2, which can be written as 2/1. This means for every 1 unit you move to the right on the graph, you must move 2 units up. Starting from the y-intercept (0, -1), moving right 1 and up 2 brings us to the point (1, 1). All four graphs show a line with this correct y-intercept and slope.
Next, we analyze the inequality symbol, which is > (greater than).
- Because the inequality is strictly “greater than” and not “greater than or equal to” (≥), the points on the line y = 2x – 1 are not part of the solution. This is represented graphically by a dashed or dotted line. This criterion immediately eliminates options a and d, which both feature a solid line.
Finally, we determine the correct shaded region. The inequality y > 2x – 1 means we are looking for all the points (x, y) where the y-value is greater than the value on the line. This corresponds to the region above the boundary line.
We can also use a test point, such as the origin (0, 0), to verify the shading. Substitute x=0 and y=0 into the inequality:
y > 2x – 1
0 > 2(0) – 1
0 > -1
This statement is true. Therefore, the point (0, 0) must be included in the shaded solution area.
Comparing the remaining options, b and c:
- Graph b has the correct dashed line, but the shading is below the line, which would represent y < 2x – 1.
- Graph c has the correct dashed line, and the shading is above the line, which includes our test point (0, 0).
Therefore, graph c is the only option that correctly represents the inequality y > 2x – 1.
